题目内容
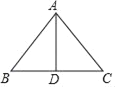
【题目】如图,在等腰三角形纸片ABC中,AB=AC=10,BC=12,将此等腰三角形纸片沿底边BC上的高AD剪成两个全等的三角形,用这两个三角形拼成一个平行四边形,则所拼出的所有平行四边形中最长的对角线的长是_____.
【答案】2![]()
【解析】
利用等腰三角形的性质,进而重新组合得出平行四边形,进而利用勾股定理求出对角线的长.
如图:
 ,
,
过点A作AD⊥BC于点D,
∵△ABC边AB=AC=10cm,BC=12cm,
∴BD=DC=6cm,
∴AD=8cm,
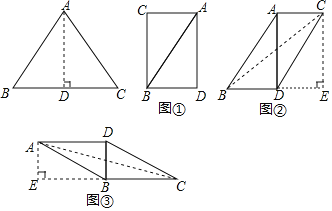
如图①所示:
可得四边形ACBD是矩形,则其对角线长为:10cm,
如图②所示:AD=8cm,
连接BC,过点C作CE⊥BD于点E,
则EC=8cm,BE=2BD=12cm,
则BC=4![]() cm,
cm,
如图③所示:BD=6cm,
由题意可得:AE=6cm,EC=2BE=16cm,
故AC=![]() cm,
cm,
![]() >4
>4![]() >10
>10
所以,最长的对角线的长是![]() .
.
故答案为:![]()

练习册系列答案
相关题目
【题目】某商店分两次购进A,B两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
购进数量(件) | 购进所需费用(元) | ||
A | B | ||
第一次 | 20 | 30 | 2800 |
第二次 | 30 | 20 | 2200 |
(1)求A、B两种商品每件的进价分别是多少元?
(2)商场决定A种商品以每件30元出售,B种商品以每件100元出售.为满足市场需求,需购进A、B两种商品共1000件,且A种商品的数量不少于B种商品数量的4倍,请你求出获利最大的进货方案,并确定最大利润.