��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У�ֱ��l����M��3��0������ƽ����y�ᣮ
��1�������ABC�������������ֱ���A����2��0����B����1��0����C����1��2������ABC����y��ĶԳ�ͼ������A1B1C1����A1B1C1����ֱ��l�ĶԳ�ͼ������A2B2C2��д����A2B2C2��������������ꣻ
��2�������P�������ǣ���a��0��������a��0����P����y��ĶԳƵ���P1����P1����ֱ��l�ĶԳƵ���P2����PP2�ij���

���𰸡�(1)A2(4��0)��B2(5��0)��C2(5,2)
��2��6.
�������������������1�����ݹ���y��ԳƵ�������ص��Ǻ����껥Ϊ�෴������������ͬ���Եõ���A1B1C1�������꣬�ֹ���ֱ��l�ĶԳ�ͼ�ε�������ص�����������ͬ��������֮�͵���3�Ķ������ɴ������A2B2C1��������������ꣻ
��2��P��P1����y��Գƣ����ù���y��ԳƵ���ص㣺�����겻�䣬�������Ϊ�෴�������P1�����꣬����ֱ��l�ķ���Ϊֱ��x=3�����öԳƵ��������P2�����꣬����PP2�ij���
�����������1����A2B2C2���������������ֱ���A2��4��0����B2��5��0����C2��5��2����
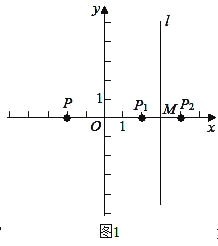
��2����ͼ1����0��a��3ʱ����P��P1����y��Գƣ�P��-a��0����
��P1��a��0����
����P1��P2����l��ֱ��x=3�Գƣ�
��P2��x��0�����ɵã�![]() =3����x=6-a��
=3����x=6-a��
��P2��6-a��0����
��PP2=6-a-��-a��=6-a+a=6��
��ͼ2����a��3ʱ��
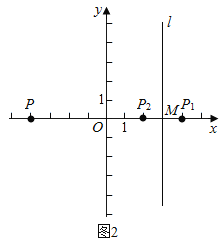
��P��P1����y��Գƣ�P��-a��0����
��P1��a��0����
����P1��P2����l��ֱ��x=3�Գƣ�
��P2��x��0�����ɵã�![]() =3����x=6-a��
=3����x=6-a��
��P2��6-a��0����
��PP2=6-a-��-a��=6-a+a=6��