题目内容
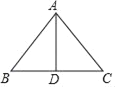
【题目】如图,△ABC中,AD平分∠BAC,EG⊥AD,分别交AB,AD,AC,BC的延长线于E,H,F,G

已知四个式子:①∠1=![]() (∠2+∠3);②∠1=
(∠2+∠3);②∠1=![]() (∠3-∠2);③∠4=
(∠3-∠2);③∠4=![]() (∠3-∠2);④∠4=
(∠3-∠2);④∠4=![]() ∠1.其中正确的式子有______.(填写序号)
∠1.其中正确的式子有______.(填写序号)
【答案】①③.
【解析】
由AD平分∠BAC,EG⊥AD,根据三角形的内角和定理得∴∠1=90°-∠BAD=90°-![]() ∠BAC,而∠BAC=180°-∠2-∠3,于是∠1=90°-
∠BAC,而∠BAC=180°-∠2-∠3,于是∠1=90°-![]() (180°-∠2-∠3)=
(180°-∠2-∠3)=![]() (∠2+∠3)故①正确;再根据三角形外角性质得∠1=∠2+∠4,得到∠4=∠1-∠2=
(∠2+∠3)故①正确;再根据三角形外角性质得∠1=∠2+∠4,得到∠4=∠1-∠2=![]() (∠2+∠3)-∠2=
(∠2+∠3)-∠2=![]() (∠3-∠2),故③正确;根据三角形内角和定理得到∠1=∠AFH,然后可得∠3=∠4+∠1,结合∠1=∠4+∠2可得
(∠3-∠2),故③正确;根据三角形内角和定理得到∠1=∠AFH,然后可得∠3=∠4+∠1,结合∠1=∠4+∠2可得![]() (∠3-∠2)=∠4,然后可得②错误;根据∠1=∠2+∠4,∠2和∠4不一定相等,可得④错误,由此得到正确答案.
(∠3-∠2)=∠4,然后可得②错误;根据∠1=∠2+∠4,∠2和∠4不一定相等,可得④错误,由此得到正确答案.
解:∵AD平分∠BAC,EG⊥AD,
∴∠BAD=∠CAD =![]() ∠BAC,∠AMF=∠ANE=90°,
∠BAC,∠AMF=∠ANE=90°,
∴∠1=90°-∠BAD=90°-![]() ∠BAC,
∠BAC,
而∠BAC=180°-∠2-∠3,
∴∠1=90°-![]() (180°-∠2-∠3)=
(180°-∠2-∠3)=![]() (∠2+∠3),故①正确;
(∠2+∠3),故①正确;
又∵∠1=∠2+∠4,
∴∠4=∠1-∠2=![]() (∠2+∠3)-∠2=
(∠2+∠3)-∠2=![]() (∠3-∠2),故③正确;
(∠3-∠2),故③正确;
∵∠1+∠BAD+∠AHE=180°,∠AFH+∠CAD+∠AHF=180°,
∴∠1=∠AFH,
∴∠3=∠4+∠CFG=∠4+∠AFH=∠4+∠1,
∴∠3-∠2=∠4+∠1-∠2
∵∠1=∠4+∠2,
∴∠3-∠2=2∠4,
∴![]() (∠3-∠2)=∠4,
(∠3-∠2)=∠4,
∴∠1=![]() (∠3-∠2)错误,即②错误;
(∠3-∠2)错误,即②错误;
∵∠1=∠2+∠4,∠2和∠4不一定相等,
∴∠4=![]() ∠1错误,即④错误.
∠1错误,即④错误.
故答案为:①③.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案