题目内容
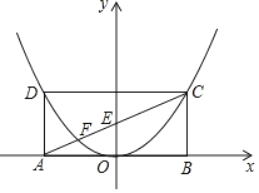
【题目】如图，矩形ABCD的顶点A、B在x轴上，点C、D落在抛物线y＝ax2（a＞0）上，对角线AC分别交y轴和抛物线于点E、F，则
的值为__．
【答案】2.
【解析】
过点F作FG⊥AB于点G，设C（m，am2），则点D（﹣m，am2），点B（m，0），点A（﹣m，0），根据待定系数法求出直线AC解析式为：
令
即可求出点G的坐标，根据平行线分线段成比例定理得到
即可求解.
解：过点F作FG⊥AB于点G，
∵抛物线y＝ax2（a＞0）图象关于y轴对称，
∴点C与点D关于y轴对称，
设C（m，am2）
∴点D（﹣m，am2），点B（m，0），点A（﹣m，0）
∴OB＝m，
∴直线AC解析式为：
∴
∴
∴
∴
∵FG∥EO∥BC
∴
故答案为：2
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
