题目内容
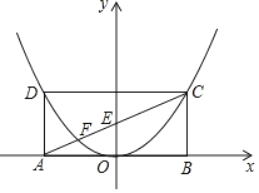
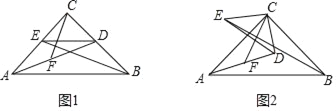
【题目】如图1,已知△ABC中,∠ACB=90°,CA=CB,点D,E分别在CB,CA上,且CD=CE,连AD,BE,F为AD的中点,连CF.
(1)求证:CF=![]() BE,且CF⊥BE;
BE,且CF⊥BE;
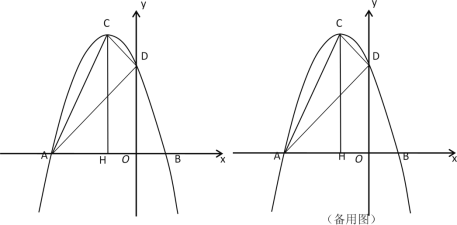
(2)将△CDE绕点C顺时针旋转一个锐角(如图2),其它条件不变,此时(1)中的结论是否仍成立?并证明你的结论.
【答案】(1见解析;(2)仍成立.
【解析】
(1)只要证明△ACD≌△BCE(SAS),即可解决问题;
(2)此时仍有CF=![]() BE、CF⊥BE.如图2中,延长CF至G,使FG=CF,连接GA,只要证明△DFC≌△AFG(SAS),△BCE≌△CAG(SAS),即可解决问题;
BE、CF⊥BE.如图2中,延长CF至G,使FG=CF,连接GA,只要证明△DFC≌△AFG(SAS),△BCE≌△CAG(SAS),即可解决问题;
解:(1)如图1中,
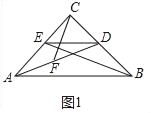
在△ACD和△BCE中,
∵CA=CB,
∠ACD=∠BCE,
CD=CE,
∴△ACD≌△BCE(SAS),
∴AD=BE、∠CAD=∠CBE,
∵F为AD中点,∠ACD=90°,
∴FC=AF=![]() AD,
AD,
∴CF=![]() BE,∠CAD=∠ACF,
BE,∠CAD=∠ACF,
∴∠CBE=∠ACF,
∴∠CBE+∠BCF=∠ACF+∠BCF=∠BCE=90°,
∴CF⊥BE;
(2)此时仍有CF=![]() BE、CF⊥BE.
BE、CF⊥BE.
理由:如图2中,延长CF至G,使FG=CF,连接GA,
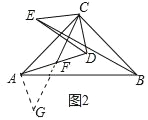
在△CDF和△GAF中,
∵DF=AF,
∠DFC=∠AFG,
CF=AF,
∴△DFC≌△AFG(SAS),
∴GA=CD,∠FDC=∠FAG,
∴AG∥DC,AG=CE,
∴∠GAC+∠DCA=180°,
又∵∠BCE+∠DCA=∠BCA+∠ACD+∠ECA=∠BCA+∠ECD=180°,
∴∠GAC=∠BCE,
在△BCE和△CAG中,
∵BC=CA,
∠BCE=∠CAG,
CE=AG,
∴△BCE≌△CAG(SAS),
∴CG=BE,∠CBE=∠ACG,
∴CF=![]() BE,∠CBE+∠BCF=∠BCA=90°,
BE,∠CBE+∠BCF=∠BCA=90°,
∴CF⊥BE.