题目内容
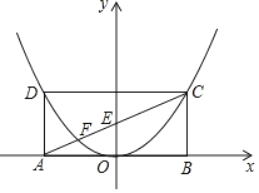
【题目】在平面直角坐标系中,抛物线y=ax2﹣3(a+1)x+2a+3(a≠0)与直线y=x﹣1交于点A和点B(点A在点B的左侧),AB=5![]() .
.
(1)求证:该抛物线必过一个定点;
(2)求该抛物线的解析式;
(3)设直线x=m与该抛物线交于点E(x1,y1),与直线AB交于点F(x2,y2),当满足y1+y2>0且y1y2<0时,求m的取值范围.
【答案】(1)见解析;(2)y=x2﹣6x+5或y=﹣![]() x2﹣x+
x2﹣x+![]() ;(3)m<1或4<m<5或﹣
;(3)m<1或4<m<5或﹣![]() <m<1或m>1.
<m<1或m>1.
【解析】
(1)将二次函数解析式进行变形,得到y=a(x2﹣3x+2)a﹣3x+3,当x2﹣3x+2=0时,即可求出函数图象过的定点.
(2)将y=x﹣1代入y=ax2﹣3(a+1)x+2a+3,根据韦达定理得到![]() 根据两点之间的距离公式即可求出
根据两点之间的距离公式即可求出![]() 的值.
的值.
(3)根据(2)中的解析式,分两种情况进行讨论即可.
解:(1)证明:∵y=ax2﹣3(a+1)x+2a+3=a(x2﹣3x+2)a﹣3x+3,
∴当x2﹣3x+2=0时,图象过定点,即:x=1或2,
∴该抛物线必过定点(1,0)、(2,﹣3);
(2)将y=x﹣1代入y=ax2﹣3(a+1)x+2a+3,整理得:ax2﹣(3a+4)x+2a+4=0,
即: ![]()
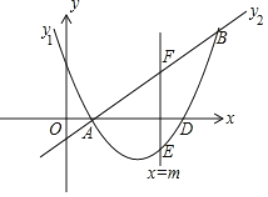
如下图,直线y=x﹣1与x轴的夹角为45°,则AB的水平距离为![]()
![]()
解得:a=1或![]()
则函数的表达式为:y=x2﹣6x+5或![]()
(3)当函数为:y1=x2﹣6x+5时,直线表达式为:y2=x﹣1,
令y1=0,则x=1或5,则点D坐标为(5,0),
①当m<1时,则y1y2<0,
当x=m时,y1+y2>0,即:m2﹣6m+5+m﹣1>0,
解得:m>4或m<1,
故:m<1;
②当1<m<5时,m2﹣6m+5+m﹣1<0,
解得:4<m或m<1,
故:4<m<5;
同理当![]() 时,
时,
![]() 或m>1;
或m>1;
综上所述:m的取值范围为:m<1或4<m<5或![]() 或m>1.
或m>1.

 阅读快车系列答案
阅读快车系列答案