Question

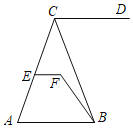
【题目】如图，在平面直角坐标系中，菱形ABCD的顶点A在x轴负半轴上，顶点B在x轴正半轴上．若抛物线p=ax2-10ax+8（a＞0）经过点C、D，则点B的坐标为________．

Answer 1

【答案】（4，0）

【解析】

根据抛物线p＝ax210ax＋8（a＞0）经过点C、D和二次函数图象具有对称性，可以求得该抛物线顶点的横坐标和CD的长，然后根据菱形的性质和勾股定理可以求得AO的长，从而可以求得OB的长，进而写出点B的坐标．

解：∵抛物线p＝ax210ax＋8＝a（x5）225a＋8，

∴该抛物线的顶点的横坐标是x＝5，当x＝0时，y＝8，

∴点D的坐标为：（0，8），

∴OD＝8，

∵抛物线p＝ax210ax＋8（a＞0）经过点C、D，CD∥AB∥x轴，

∴CD＝5×2＝10，

∴AD＝10，

∵∠AOD＝90°，OD＝8，AD＝10，

∴AO＝，

∵AB＝10，

∴OB＝10AO＝106＝4，

∴点B的坐标为（4，0），

故答案为：（4，0）