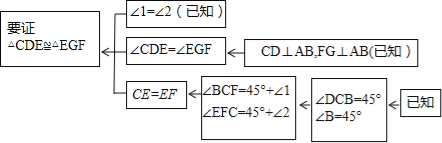
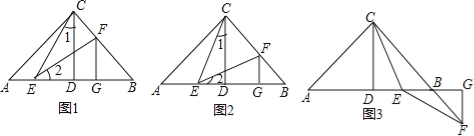
��Ŀ����
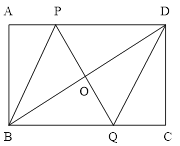
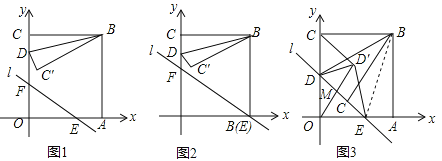
����Ŀ����2016�㽭ʡ�����У���ͼ1����ֱ������ϵxoy�У�ֱ��l��y=kx+b��x�ᣬy���ڵ�E��F����B�������ǣ�2��2��������B�ֱ���x�ᡢy��Ĵ��ߣ�����ΪA��C����D���߶�CO�ϵĶ��㣬��BDΪ�Գ��ᣬ������BCD����ԳƵ���BC��D��
��1������CBD=15��ʱ�����C�������꣮
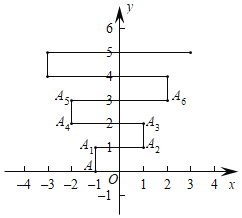
��2����ͼ1�е�ֱ��l������A����![]() ʱ����ͼ2�������D��C��O���˶������У��߶�BC��ɨ����ͼ������OAF�ص����ֵ������
ʱ����ͼ2�������D��C��O���˶������У��߶�BC��ɨ����ͼ������OAF�ص����ֵ������
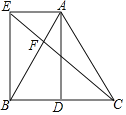
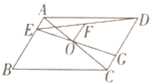
��3����ͼ1�е�ֱ��l������D��C��ʱ����ͼ3������DEΪ�Գ��ᣬ������DOE����ԳƵ���DO��E������O��C��O��O�����Ƿ���ڵ�D��ʹ����DO��E����CO��O���ƣ������ڣ����k��b��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��C�䣨![]() ��1������2��
��1������2��![]() ����3�����ڣ�k=
����3�����ڣ�k=![]() ��b=1��
��b=1��
�����������⣨1�����÷��۱任�����ʵó���CBD=��C��BD=15�㣬C��B=CB=2�������ó�CH�ij��������ó��𰸣�
��2���������ֱ��AF�Ľ���ʽ�������ó���D��O�غ�ʱ����C����A�غϣ���BC��ɨ����ͼ������OAF�غϲ����ǹ��Σ�������ɣ�
��3����������ó���DO��E����COO�����ƣ�����COO������Rt���������ó�Rt��BAE��Rt��BC��E��HL���������ù��ɶ������EO�ij������ó��𰸣�
�����������1���ߡ�CBD�ա�C��BD�����CBD=��C��BD=15�㣬C��B=CB=2�����CBC��=30������ͼ1����C��H��BC��H����C��H=1��HB=![]() ����CH=
����CH=![]() �����C������������
�����C������������![]() ��1����
��1����
��2����ͼ2����A��2��0����![]() �������ֱ��AF�Ľ���ʽΪ��
�������ֱ��AF�Ľ���ʽΪ��![]() ����b=
����b=![]() ����ֱ��AF�Ľ���ʽΪ��
����ֱ��AF�Ľ���ʽΪ��![]() �����OAF=30�㣬��BAF=60�㣬���ڵ�D��C��O���˶������У�BC��ɨ����ͼ�������Σ��൱D��O�غ�ʱ����C����A�غϣ���BC��ɨ����ͼ������OAF�غϲ����ǹ��Σ���C����ֱ��
�����OAF=30�㣬��BAF=60�㣬���ڵ�D��C��O���˶������У�BC��ɨ����ͼ�������Σ��൱D��O�غ�ʱ����C����A�غϣ���BC��ɨ����ͼ������OAF�غϲ����ǹ��Σ���C����ֱ��![]() ��ʱ��BC��=BC=AB�����ABC���ǵȱ������Σ���ʱ��ABC��=60�㣬���ص����ֵ�����ǣ�
��ʱ��BC��=BC=AB�����ABC���ǵȱ������Σ���ʱ��ABC��=60�㣬���ص����ֵ�����ǣ�![]() =
=![]() ��
��
��3����ͼ3����OO����DE���ڵ�M����O��M=OM��OO����DE������DO��E����COO�����ƣ�����COO������Rt�����ڵ�D��C��O���˶������У���COO������Ȼֻ�ܡ�CO��O=90�㣬��CO����DE����CD=OD=1����b=1������BE������Գ��Կ�֪C��D=CD��BC��=BC=BA����BC��E=��BCD=��BAE=90������Rt��BAE��Rt��BC��E������BE=BE��AB=BC�䣬��Rt��BAE��Rt��BC��E��HL������AE=C��E����DE=DC��+C��E=DC+AE����OE=x����AE=2��x����DE=DC+AE=3��x���ɹ��ɶ����ã�![]() ����ã�x=
����ã�x=![]() ����D��0��1����E��
����D��0��1����E��![]() ��0������
��0������![]() ����ã�k=
����ã�k=![]() ������ڵ�D��ʹ��DO��E����COO�����ƣ���ʱk=
������ڵ�D��ʹ��DO��E����COO�����ƣ���ʱk=![]() ��b=1��
��b=1��


 ���ſ����ϵ�д�
���ſ����ϵ�д� ���Ŀ����ϵ�д�
���Ŀ����ϵ�д� ������ӱ������ͯ������ϵ�д�
������ӱ������ͯ������ϵ�д� A�ӽ��� ϵ�д�
A�ӽ��� ϵ�д�