题目内容
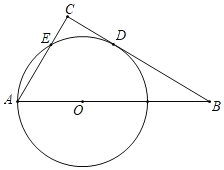
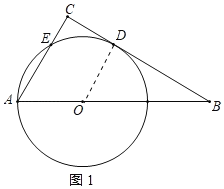
【题目】如图,已知Rt△ABC中,CAB=60°,点O为斜边AB上一点,且OA=2,以OA为半径的⊙O与BC相切于D,与AC交于点E,连接AD.
(1)求线段CD的长;
(2)求⊙O与Rt△ABC重叠部分的面积.(结果保留准确值)
【答案】(1)CD=![]() ;(2)
;(2)![]() .
.
【解析】
(1)连接OD,由切线的性质和直角三角形的性质得出OB=2OD=4,BD=![]() OD=2
OD=2![]() ,得出AB=OA+OB=6,AC=
,得出AB=OA+OB=6,AC=![]() AB=3,BC=
AB=3,BC=![]() AC=3
AC=3![]() ,即可得出结果;
,即可得出结果;
(2)连接OE,证出△OAE是等边三角形,得出∠AOE=60°,∠EOG=120°,作EF⊥OA于F,则OF=1,EF=![]() OF=
OF=![]() ,⊙O与Rt△ABC重叠部分的面积=△AOE的面积+扇形OEDG的面积,即可得出结果,
,⊙O与Rt△ABC重叠部分的面积=△AOE的面积+扇形OEDG的面积,即可得出结果,
(1)连接OD,如图1所示:
∵以OA为半径的⊙O与BC相切于D,
∴∠ODB=90°.
∵OD=OA=2,∠C=90°,∠CAB=60°,
∴∠B=30°,
∴OB=2OD=4,BD=![]() OD=2
OD=2![]() ,
,
∴AB=OA+OB=6,
∴AC=![]() AB=3,
AB=3,
∴BC=![]() AC=3
AC=3![]() ,
,
∴CD=BC﹣BD=![]() ;
;
(2)连接OE,如图2所示:
则OA=OE.
∵∠CAB=60°,
∴△OAE是等边三角形,
∴∠AOE=60°,
∴∠EOG=120°,
作EF⊥OA于F,
则OF=1,EF=![]() OF=
OF=![]() ,
,
∴⊙O与Rt△ABC重叠部分的面积=△AOE的面积+扇形OEDG的面积=![]() ×2×
×2×![]() +
+![]() =
=![]() +
+![]() .
.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案【题目】费尔兹奖是国际上享有崇高荣誉的一个数学奖项,每4年评选一次,在国际数学家大会上颁给有卓越贡献的年龄不超过40岁的年轻数学家,美籍华人丘成桐1982年获得费尔兹奖.为了让学生了解费尔兹奖得主的年龄情况,我们查取了截止到2018年60名费尔兹奖得主获奖时的年龄数据,并对数据进行整理、描述和分析.下面给出了部分信息.
a.截止到2018年费尔兹奖得主获奖时的年龄数据的频数分布直方图如图1(数据分成5组,各组是28≤x<31,31≤x<34,34≤x<37,37≤x<40,x≥40):
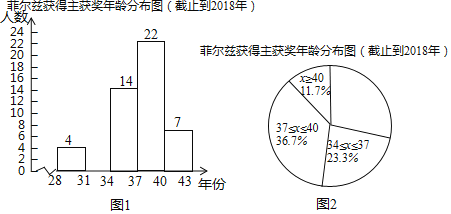
b.如图2,在a的基础上,画出扇形统计图;
c.截止到2018年费尔兹奖得主获奖时的年龄在34≤x<37这一组的数据是:
36 | 35 | 34 | 35 | 35 | 34 | 34 | 35 | 36 | 36 | 36 | 36 | 34 | 35 |
d.截止到2018年时费尔兹奖得主获奖时的年龄的平均数、中位数、众数如下:
年份 | 平均数 | 中位数 | 众数 |
截止到2018 | 35.58 | m | 37,38 |
根据以上信息,回答下列问题:
(1)依据题意,补全频数直方图;
(2)31≤x<34这组的圆心角度数是度,并补全扇形统计图;
(3)统计表中中位数m的值是;
(4)根据以上统计图表试描述费尔兹奖得主获奖时的年龄分布特征.