题目内容
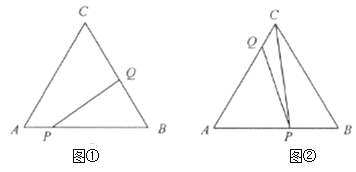
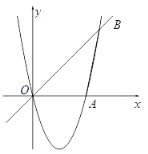
【题目】如图(1),二次函数![]() 的图象与
的图象与![]() 轴、直线
轴、直线![]() 的交点分别为点
的交点分别为点![]() 、
、![]() .
.

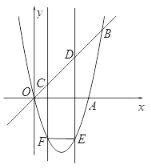

图(1) 图(2) (备用图)
(1)![]()
![]() _________,
_________,![]()
![]() _________,
_________,![]() =_________
=_________![]() ;
;
(2)连接AB,点![]() 是抛物线上一点(异于点A),且
是抛物线上一点(异于点A),且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图(2),点![]() 、
、![]() 是线段
是线段![]() 上的动点,且
上的动点,且![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() .
.
①过点![]() 、
、![]() 分别作
分别作![]() 轴的垂线,与抛物线相交于点
轴的垂线,与抛物线相交于点![]() 、
、![]() ,连接
,连接![]() .当
.当![]() 取得最大值时,求
取得最大值时,求![]() 的值并判断四边形
的值并判断四边形![]() 的形状;
的形状;
②连接![]() 、
、![]() ,求
,求![]() 为何值时,
为何值时,![]() 取得最小值,并求出这个最小值.
取得最小值,并求出这个最小值.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)①
;(3)①![]() 时,
时,![]() 取得最大值;四边形
取得最大值;四边形![]() 是平行四边形;②当
是平行四边形;②当![]() 时,
时,![]() 最小,这个最小值为
最小,这个最小值为![]() .
.
【解析】
(1)利用坐标点过二次函数图像,待定系数法即可得.
直线OB是正比例函数![]() ,
,![]() ,可得出直线与x轴的夹角.
,可得出直线与x轴的夹角.
(2)通过找![]() 的对称点
的对称点![]() 作辅助线,通过图像的几何特征联立方程求出直线解析式,直线一次函数与二次函数的交点即为所求的坐标点.
作辅助线,通过图像的几何特征联立方程求出直线解析式,直线一次函数与二次函数的交点即为所求的坐标点.
(3)①找出线段关系式,即线段和![]() 以m的关系式,问题变成以m为变量的函数极值问题,通过配方法解得.
以m的关系式,问题变成以m为变量的函数极值问题,通过配方法解得.
②动点线段和的极值问题,关键是找对称点,通过“两点间,线段最短”的思路添加辅助线求得.
(1)
因为二次函数![]() 图像经过
图像经过![]() 、
、![]()
∴![]() 解得
解得 ![]() ,
,![]() ,
,
又∵正比例函数![]() ,
,![]() ,可得出直线与x轴的夹角
,可得出直线与x轴的夹角![]() ;
;
(2)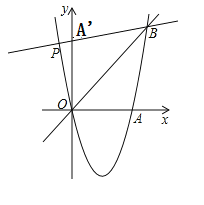
作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,直线
,直线![]()
∵![]() ,
,![]() ,
,
∴![]() ∴
∴![]()
又∵![]() ,设
,设![]() 的解析式为
的解析式为![]()
则有![]()
∴求出直线![]() 的解析式为
的解析式为![]() ,
,
解方程组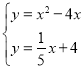 ,得
,得![]()
(3)①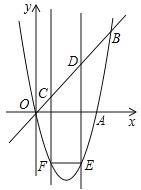
∵点![]() 的横坐标为
的横坐标为![]() ,且
,且![]() 轴,
轴,
∴![]() ,
,![]() ,
,
又∵![]() ,且
,且![]() 是线段
是线段![]() 上的一动线段,
上的一动线段,
span>∴![]() ,
,![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]()
![]()
![]()
∴当![]() 时,
时,![]() 取得最大值;
取得最大值;
此时,![]() ,
,![]()
∴![]()
∴四边形![]() 是平行四边形.
是平行四边形.
②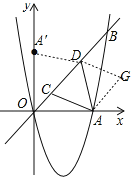
如图所示,过点![]() 作
作![]() 的平行线,过点
的平行线,过点![]() 作
作![]() 的平行线,交于点
的平行线,交于点![]() ,则四边形
,则四边形![]() 是平行四边形,
是平行四边形,
∴![]()
∵点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,连接
对称,连接![]() ,
,![]() ,则
,则![]() .
.
∴![]()
∴当![]() ,
,![]() ,
,![]() 三点共线时,
三点共线时,![]() 最短,此时
最短,此时![]() 最短,
最短,
∵![]() ,
,![]() ,
,![]()
![]()
∴![]() ,
,![]() ,
,
![]()
得出直线![]() 的解析式为
的解析式为![]() ,
,
解方程组 ,可得
,可得![]() ,
,
∴![]() ,而
,而![]()
∴![]() ,
,![]() ,
,
![]() ,
,
故当![]() 时,
时,![]() 最小,这个最小值为
最小,这个最小值为![]() .
.

 巧学巧练系列答案
巧学巧练系列答案【题目】某校举行“汉字听写”比赛,每位学生听写汉字40个,比赛结束后随机抽查部分学生听写“正确的字数”,以下是根据抽查结果绘制的统计图表.
频数分布表
组别 | 正确的字数 | 人数 |
| 0.5~8.5 | 10 |
| 8.5~16.5 | 15 |
| 16.5~24.5 | 25 |
| 24.5~32.5 |
|
| 32.5~40.5 |
|
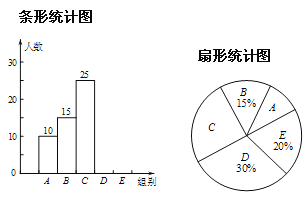
根据以上信息解决下列问题:
(1)补全条形统计图;
(2)扇形统计图中“![]() 组”所对应的圆心角的度数是_________;
组”所对应的圆心角的度数是_________;
(3)若该校共有1210名学生,如果听写正确的字数少于25,则定为不合格;请你估计这所学校本次比赛听写不合格的学生人数.