题目内容
【题目】如图,将边长为1的正方形纸片ABCD折叠,使点B的对应点M落在边CD上(不与点C、D重合),折痕为EF,AB的对应线段MG交AD于点N.以下结论正确的有( )①∠MBN=45°;②△MDN的周长是定值;③△MDN的面积是定值.

A.①②B.①③C.②③D.①②③
【答案】A
【解析】
连接BM、BN,作BP⊥MN于P.只要证明△BMP≌△BMC,可得MP=MC,∠PBM=∠CBM,同理可证:NA=NP,∠ABN=∠PBN,由此可判断①②正确.
连接BG、BE,作BP⊥EF于P,如图所示:
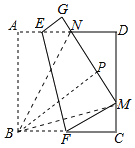
由折叠性质可得:BF=FM,
∴∠MBF=∠FMB,
∵四边形ABCD是正方形,
∴∠C=∠ABC=∠NMF=90°,
∴∠CBM+∠BMC=90°,∠BMF+∠NMB=90°,
∴∠BMC=∠NMB,
又∵BP⊥MN,BC⊥DC,
∴BP=BC,且∠BMC=∠NMB,BM=BM
∴△BPM≌△BCM(SAS),
∴MP=MC,∠PBM=∠CBM,
同理可证:NA=NP,∠ABN=∠PBN,
∴△MND的周长=DN+DM+MN=DN+AN+DM+CM=AD+CD=2,
∴△DGE的周长始终为定值.
∵∠ABN+∠PBN+∠PBM+∠CBM=90°
∴∠MBN=45°;
∵DM,DN的值不确定,
∴△MDN的面积不确定,
∴③错误.
故①②正确
故选:A.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目