题目内容
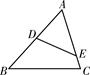
如图,在YABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,DE:EC=2:3,则S△DEF:S△ABF=( )
| A.2:3 | B.4:9 | C.2:5 | D.4:25 |
D.
解析试题分析:先根据平行四边形的性质及相似三角形的判定定理得出△DEF∽△BAF,从而DE:AB=DE:DC=2:5,所以S△DEF:S△ABF=4:25
试题解析:∵四边形ABCD是平行四边形,
∴AB∥CD,BA=DC
∴∠EAB=∠DEF,∠AFB=∠DFE,
∴△DEF∽△BAF,
∴DE:AB=DE:DC=2:5,
∴S△DEF:S△ABF=4:25,
考点:1.相似三角形的判定与性质;2.三角形的面积;3.平行四边形的性质.

练习册系列答案
相关题目
如图,点,,,的坐标分别是(1,7),(1,1),(4,1),(6,1),以,,为顶点的三角形与△相似,则点的坐标不可能是
| A.(6,0) | B.(6,3) | C.(6,5) | D.(4,2) |
已知△ABC和△DEF相似,且△ABC的三边长为3、4、5,如果△DEF的周长为6,那么下列不可能是△DEF一边长的是( )
| A.1.5; | B.2; | C.2.5; | D.3. |
如图,在平行四边形ABCD中,E为CD上一点,DE:CE=2:3,连结AE、BE、BD且AE,BD交于点F,则S△DEF:S△ADF:S△ABF等于( )
| A.2:3:5 | B.4:9:25 | C.4:10:25 | D.2:5:25 |