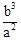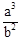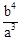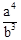题目内容
如图，菱形ABCD中，点M，N在AC上，ME⊥AD，NF⊥AB.若NF=NM=2，ME=3，则AN=（ ）
A．3 B．4 C．5 D．6
B.
解析试题分析：设AN=x,则AM=x+2,根据菱形的性质：对角线互相垂直平分，且平分一组对角.所以有∠NAF=∠MAE,因为ME⊥AD，NF⊥AB,所以∠AEM=∠AFN=90°,根据相似三角形的判定：有两组角对应相等的两个三角形相似.可知△AME∽△ANF,所以有比例式：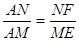
,即
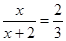，解得：x=4,故选B.
考点：1、相似三角形的性质；2、相似三角形的判定.
练习册系列答案
相关题目
如图，E是平行四边形ABCD的边BC的延长线上的一点，连结AE交CD于F，则图中共有相似三角形（ ）
| A．1对 | B．2对 | C．3对 | D．4对 |
如图，在YABCD中，E为CD上一点，连接AE、BD，且AE、BD交于点F，DE：EC=2:3，则S△DEF:S△ABF=（ ）
| A．2：3 | B．4：9 | C．2：5 | D．4：25 |
直线l1∥l2∥l3，且l1与l2的距离为1，l2与l3的距离为3，把一块含有45°角的直角三角形如图放置，顶点A，B，C恰好分别落在三条直线上，AC与直线l2交于点D，则线段BD的长度为( )
A． | B． | C． | D． |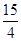
如图，在直角坐标系中，矩形OABC的顶点O在坐标原点，边OA在x轴上，OC在y轴上，如果矩形
与矩形OABC关于点O位似，且矩形的面积等于矩形OABC面积的
，那么点B/的坐标是( ).
A． | B． |
C．或 | D． 或 |
，则EF＋CF的长为（ ）
