题目内容
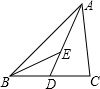
如图,延长长方形的边BC至E点,使BC=2CE,若△CDE的面积是1,则长方形ABCD的面积是______.
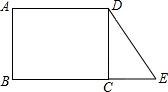

在长方形ABCD中,∠BCD=90°.
∵点E在BC边的延长线上,
∴∠DCE=90°,
∴S△DCE=
CE•DC=1,即CE•DC=2.
又∵BC=2CE,
∴S长方形ABCD=BC•DC=2CE•DC=2×2=4,即长方形ABCD的面积是4.
故答案是:4.
∵点E在BC边的延长线上,
∴∠DCE=90°,
∴S△DCE=
| 1 |
| 2 |
又∵BC=2CE,
∴S长方形ABCD=BC•DC=2CE•DC=2×2=4,即长方形ABCD的面积是4.
故答案是:4.

练习册系列答案
相关题目