题目内容
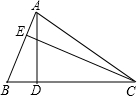
如图,在△ABC中,点D为边BC的中点,点E为线段AD上一点,且满足AE=2ED,则△ABC与△BDE的面积之比为______.
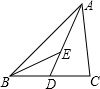

∵点D为边BC的中点,
∴S△ABD=S△ACD=
S△ABC,
∵AE=2ED
∴S△BDE=
S△BEA,
又∵S△BDE+S△BEA=S△ABD,
即:S△BDE+2S△BDE=S△ABD=
S△ABC,
∴S△BDE=
S△ABC.
即:△ABC与△BDE的面积之比为6:1,
故答案为6:1.
∴S△ABD=S△ACD=
| 1 |
| 2 |
∵AE=2ED
∴S△BDE=
| 1 |
| 2 |
又∵S△BDE+S△BEA=S△ABD,
即:S△BDE+2S△BDE=S△ABD=
| 1 |
| 2 |
∴S△BDE=
| 1 |
| 6 |
即:△ABC与△BDE的面积之比为6:1,
故答案为6:1.

练习册系列答案
相关题目