Question

【题目】在等边△ABC中，点P，Q是BC边上的两个动点（不与点B、C重合），且AP＝AQ．

（1）如图1，已知，∠BAP＝20°，求∠AQB的度数；

（2）点Q关于直线AC的对称点为M，分别联结AM、PM；

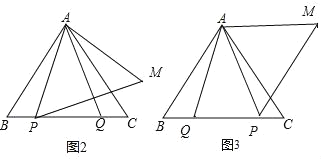
①当点P分别在点Q左侧和右侧时，依据题意将图2、图3补全（不写画法）；

②小明提出这样的猜想：点P、Q在运动的过程中，始终有PA＝PM．经过小红验证，这个猜想是正确的，请你在①的点P、Q的两种位置关系中选择一种说明理由．

Answer 1

【答案】（1）80° （2）①答案见解析 ②答案见解析

【解析】

（1）先利用三角形外角定理得到∠APQ的值，再利用等边对等角转化即可；

（2）①根据题中所述步骤补全图形即可；

②选择点P在点Q的左侧，QM交AC于点H，证明 △AQH≌△AMH，再证明AP＝AM，最后证明△APM是等边三角形即可.

解：（1）∵AP＝AQ，

∴∠APQ＝∠AQP，

∵△ABC是等边三角形，

∴∠B＝∠C＝60°，

∵∠BAP＝20°，

∴∠AQB＝∠APQ＝∠BAP+∠B＝80°；

（2）①如图2，3所示：

②PA＝PM，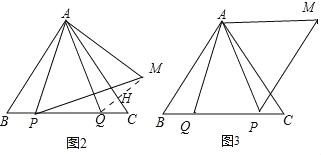

点P在点Q的左侧，QM交AC于点H，

∵点Q关于直线AC的对称点为M，

∴QH＝MH，∠AHQ＝∠AHM，

∵AH＝AH，

∴△AQH≌△AMH（SAS），

∴AQ＝AM，∠QAH＝∠MAH，

∵AP＝AQ，

∴AP＝AM，

∵∠BAP＝∠CAQ，

∴∠QAH＝∠MAH＝∠BAP，

∴∠PAM＝∠PAQ+∠QAH+∠MAH＝∠PAQ+∠QAH+∠BAP＝∠BAC＝60°，

∴△APM是等边三角形，

∴PA＝PM．