ЬтФПФкШн
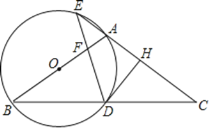
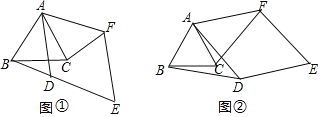
ЁОЬтФПЁПвбжЊЁїABCЪЧЕШБпШ§НЧаЮЃЌЫФБпаЮADEFЪЧСтаЮЃЌЁЯADE=120ЁуЃЈADЃОABЃЉЃЎ
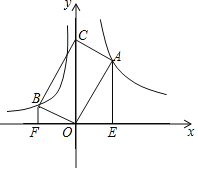
ЃЈ1ЃЉШчЭМЂйЃЌЕБADгыБпBCЯрНЛЃЌЕуDгыЕуFдкжБЯпACЕФСНВрЪБЃЌBDгыCFЕФЪ§СПЙиЯЕЮЊ___________ЃЎ
ЃЈ2ЃЉНЋЭМЂйжаЕФСтаЮADEFШЦЕуAдкЦНУцФкФцЪБеыа§зЊІСЃЈ0ЁуЃМІСЃМ180ЁуЃЉЃЎ
ЂёЃЎХаЖЯЃЈ1ЃЉжаЕФНсТлЪЧЗёШдШЛГЩСЂЃЌЧыРћгУЭМЂкжЄУїФуЕФНсТлЃЎ
ЂђЃЎШєAC=4ЃЌAD=6ЃЌЕБЁїACEЮЊжБНЧШ§НЧаЮЪБЃЌжБНгаДГіCEЕФГЄЖШЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉIЃЈ1ЃЉжаЕФНсТлШдШЛГЩСЂЃЌРэгЩЯъМћНтЮіЃЛII
ЃЛЃЈ2ЃЉIЃЈ1ЃЉжаЕФНсТлШдШЛГЩСЂЃЌРэгЩЯъМћНтЮіЃЛII![]() Лђ
Лђ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЕШЪНЕФаджЪЕУГіЁЯBAD=ЁЯCAFЃЌРћгУSASжЄУїЁїABDгыЁїACFШЋЕШЃЌдйРћгУШЋЕШШ§НЧаЮЕФаджЪЕУГіМДПЩЃЛ
ЃЈ2ЃЉIЃЎИљОнЕШЪНЕФаджЪЕУГіЁЯBAD=ЁЯCAFЃЌРћгУSASжЄУїЁїABDгыЁїACFШЋЕШЃЌдйРћгУШЋЕШШ§НЧаЮЕФаджЪЕУГіМДПЩЃЛ
IIЃЎЕБЁїACEЪЧжБНЧШ§НЧаЮЪБЃЌДцдкСНжжЧщПіЃК
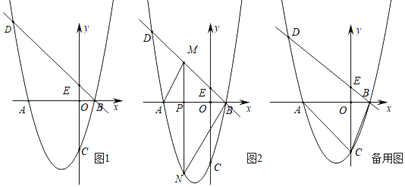
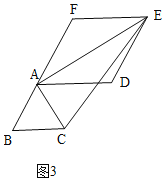
ЂйШчЭМ2ЃЌЕБЁЯACE=90ЁуЪБЃЌЂкШчЭМ3ЃЌЕБЁЯEAC=90ЁуЪБЃЌЙДЙЩЖЈРэМДПЩЕУCEЕФГЄЃЎ
ЃЈ1ЃЉНтЃКШчЭМЂйЃЌЁпЫФБпаЮADEFЪЧСтаЮЃЌЁЯADE=120ЁуЃЌ
ЁрAD=AFЃЌЁЯDAF=60ЁуЃЌ
ЁрЁЯDAC+ЁЯCAF=60ЁуЃЌ
ЁпЁїABCЪЧЕШБпШ§НЧаЮЃЌ
ЁрAB=ACЃЌЁЯBAC=60ЁуЃЌ
ЁрЁЯBAD+ЁЯDAC=60ЁуЃЌ
ЁрЁЯBAD=ЁЯCAFЃЌ
ЁрЁїBADЁеЁїCAFЃЈSASЃЉЃЌ
ЁрBD=CFЃЛ
ЙЪД№АИЮЊЃКBD=CFЃЛ
ЃЈ2ЃЉIЃЎЃЈ1ЃЉжаЕФНсТлШдШЛГЩСЂЃЎ
жЄУїЃКШчЭМЂкЃЌЁпЁїABCЪЧЕШБпШ§НЧаЮЃЌ
ЁрAB=ACЃЌЁЯBAC=60ЁуЃЌ
дкСтаЮADEFжаЃЌ
ЁрAD=AFЃЌAFЁЮDEЃЌ
ЁрЁЯDAF=180Ёу-ЁЯADE=180Ёу-120Ёу=60ЁуЃЌ
ЁрЁЯBAC=ЁЯDAFЃЌ
МДЁЯBAC+ЁЯCAD=ЁЯDAF+ЁЯCADЃЌ
ЁрЁЯBAD=ЁЯCAFЃЌ
ЁрЁїBADЁеЁїCAFЃЌ
ЁрBD=CFЃЛ
IIЃЎЕБЁїACEЪЧжБНЧШ§НЧаЮЪБЃЌДцдкСНжжЧщПіЃК
ЂйШчЭМ2ЃЌЕБЁЯACE=90ЁуЪБЃЌЙ§FзїFGЁЭAEгкGЃЌ
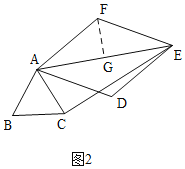
ЁпЫФБпаЮADEFЪЧСтаЮЃЌ
ЁрAF=FEЃЌЁЯAFE=ЁЯADE=120ЁуЃЌ
ЁрЁЯAFG=60ЁуЃЌ
ЁрЁЯFAG=30ЁуЃЌ
ЁпAF=AD=6ЃЌ
ЁрFG=3ЃЌ
ЁрAG=3![]() ЃЌ
ЃЌ
ЁрAE=2AG=6![]() ЃЌ
ЃЌ
RtЁїACEжаЃЌCE=![]() =
=![]() ЃЛ
ЃЛ
ЂкШчЭМ3ЃЌЕБЁЯEAC=90ЁуЪБЃЌЭЌРэЕУЃКAE=6![]() ЃЌ
ЃЌ
гЩЙДЙЩЖЈРэЕУЃКCE=![]() =
=![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃЌCEЕФГЄЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ

 ДКгъНЬг§ЭЌВНзїЮФЯЕСаД№АИ
ДКгъНЬг§ЭЌВНзїЮФЯЕСаД№АИЁОЬтФПЁПФГбЇаЃАЫЁЂОХСНИіФъМЖИїгабЇЩњ180ШЫЃЌЮЊСЫНтетСНИіФъМЖбЇЩњЕФЬхжЪНЁПЕЧщПіЃЌНјааСЫГщбљЕїВщЃЌОпЬхЙ§ГЬШчЯТЃК
ЁЁЁЁЪеМЏЪ§Он
ДгАЫЁЂОХСНИіФъМЖИїЫцЛњГщШЁ20УћбЇЩњНјааЬхжЪНЁПЕВтЪдЃЌВтЪдГЩМЈЃЈАйЗжжЦЃЉШчЯТЃК
АЫФъМЖ | 78 | 86 | 74 | 81 | 75 | 76 | 87 | 70 | 75 | 90 |
75 | 79 | 81 | 70 | 74 | 80 | 86 | 69 | 83 | 77 | |
ОХФъМЖ | 93 | 73 | 88 | 81 | 72 | 81 | 94 | 83 | 77 | 83 |
80 | 81 | 70 | 81 | 73 | 78 | 82 | 80 | 70 | 40 |
ећРэЁЂУшЪіЪ§Он
НЋГЩМЈАДШчЯТЗжЖЮећРэЁЂУшЪіетСНзщбљБОЪ§ОнЃК
ГЩМЈЃЈxЃЉ | 40ЁмxЁм49 | 50ЁмxЁм59 | 60ЁмxЁм69 | 70ЁмxЁм79 | 80ЁмxЁм89 | 90ЁмxЁм100 |
АЫФъМЖШЫЪ§ | 0 | 0 | 1 | 11 | 7 | 1 |
ОХФъМЖШЫЪ§ | 1 | 0 | 0 | 7 | 10 | 2 |
ЃЈЫЕУїЃКГЩМЈ80ЗжМАвдЩЯЮЊЬхжЪНЁПЕгХауЃЌ70ЁЋ79ЗжЮЊЬхжЪНЁПЕСМКУЃЌ60ЁЋ69ЗжЮЊЬхжЪНЁПЕКЯИёЃЌ60ЗжвдЯТЮЊЬхжЪНЁПЕВЛКЯИёЃЉ
ЁЁЁЁЗжЮіЪ§Он
СНзщбљБОЪ§ОнЕФЦНОљЪ§ЁЂжаЮЛЪ§ЁЂжкЪ§ЁЂЗНВюШчБэЫљЪОЃК
ФъМЖ | ЦНОљЪ§ | жаЮЛЪ§ | жкЪ§ | ЗНВю |
АЫФъМЖ | 78.3 | 77.5 | 75 | 33.6 |
ОХФъМЖ | 78 | 80.5 | a | 52.1 |
ЃЈ1ЃЉБэИёжаaЕФжЕЮЊ______ЃЛ
ЃЈ2ЃЉЧыФуЙРМЦИУаЃОХФъМЖЬхжЪНЁПЕгХауЕФбЇЩњШЫЪ§ЮЊЖрЩйЃП
ЃЈ3ЃЉИљОнвдЩЯаХЯЂЃЌФуШЯЮЊФФИіФъМЖбЇЩњЕФЬхжЪНЁПЕЧщПіИќКУвЛаЉЃПЧыЫЕУїРэгЩЃЎЃЈЧыДгСНИіВЛЭЌЕФНЧЖШЫЕУїЭЦЖЯЕФКЯРэадЃЉ