Question

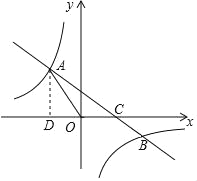
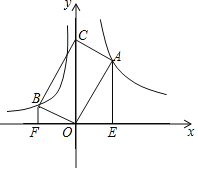
【题目】如图，点A、B在x轴的上方，∠AOB＝90°，OA、OB分别与函数、的图象交于A、B两点，以OA、OB为邻边作矩形AOBC．当点C在y轴上时，分别过点A和点B作AE⊥x轴，BF⊥x轴，垂足分别为E、F，则＝_______．

Answer 1

【答案】4

【解析】

根据题意四边形AOBC是矩形，得到OF=OE,因为OA、OB分别与函数y= 、y=- 的图象交于A、B两点，得到AE= , BF= ，即可解答

∵AE⊥x轴，BF⊥x轴，

∴AE∥y轴∥BF,

∵四边形AOBC是矩形，

∴△AOC≌△BCO,

∴ COFO= COOE,

∴OF=OE,

∵OA、OB分别与函数y= 、y=- 的图象交于A、B两点，

∴ BFOF=2, AEOE=8

∴AE= , BF=

∴

故答案为4