题目内容
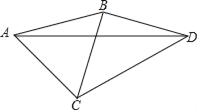
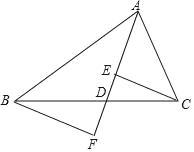
【题目】如图，AD是△ABC的中线，E，F分别是AD和AD延长线上的点，且DE=DF，连接BF，CE，下列说法中正确的个数是（ ）
①CE=BF；②△ABD和△ADC的面积相等；③BF∥CE；④CE，BF均与AD垂直
A. 4个 B. 3个 C. 2个 D. 1个
【答案】B
【解析】
根据已知条件已证△BDF≌△CDE，根据全等三角形的性质可判定①正确；由△BDF≌△CDE可得∠CED=∠BFD，∠CED与∠BFD不一定是直角，即故CE，BF均与AD不一定垂直，可判定④错误；根据三角形中线的性质可判定②正确；由△BDF≌△CDE，可知∠FBD=∠ECD，所以BF∥CE，即可判定③正确．
解：∵AD是△ABC的中线，
∴BD=CD，又∠CDE=∠BDF，DE=DF，
∴△BDF≌△CDE（SAS），
∴∠CED=∠BFD，但不一定是直角，即故CE，BF均与AD不一定垂直，故④错误；
由△BDF≌△CDE，可知CE=BF，故①正确；
∵AD是△ABC的中线，
∴△ABD和△ACD等底等高，
∴△ABD和△ACD面积相等，故②正确；
由△BDF≌△CDE，可知∠FBD=∠ECD
∴BF∥CE，故③正确．
故选B．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
