题目内容
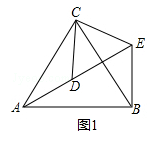
【题目】如图,∠BAD=∠BDA=15°,∠CAD=45°,∠CDA=30°,试判断三角形ABC的形状,并说明理由.
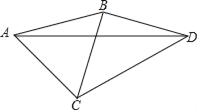
【答案】三角形ABC为等边三角形,理由详见解析.
【解析】
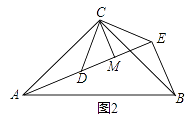
△ABC为等边三角形,将△ABC绕B点旋转,使A点与D点重合,得△ABC′,连接CC′,则得到△ABC≌△DBC′,再由角的关系及等腰三角形的性质证明△ACD≌△C′DC,△ABD≌△CBC′,得出∠∠ABC=60°,从而判定△ABC为等边三角形.
解:三角形ABC为等边三角形.
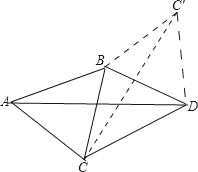
因此将△ABC绕B点旋转,使A点与D点重合,连接CC′,则△ABC≌△DBC′,
∴BC=BC′,AC=DC′,∠BDC′=∠BAC,∠ABC=∠DBC′,
∵∠BAD=∠BDA=15°,∠CAD=45°,∠CDA=30°,
∴∠CDC′=∠CDA+∠BDA+∠BDC′=∠CDA+∠BDA+∠ABC=∠CDA+∠BDA+∠CAD+∠BAD=30°+15°+45°+15°=105°,
∴∠ACD=180°-∠CAD-∠CDA=180°-45°-30°=105°,
又CD=CD,
∴△ACD≌△C′DC,
∴AD=CC′,
∠CBC′=∠DBC′+∠CBD,∠ABD=∠ABC+∠CBD,
∵∠ABC=∠DBC′,
∴∠CBC′=∠ABD=180°-15°-15°=150°,
∴∠BCC′=∠BC′C=15°,
∴△ABD≌△CBC′,
∴AB=BC,
∴∠ACB=∠BAC=∠BAD+∠CAD=15°+45°=60°,
∴∠ABC=60°,
∴△ABC为等边三角形.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目