Question

【题目】如图，点O为原点，⊙O的半径为1，点A的坐标为（2，0），动点B在⊙O上，以AB为边作等边△ABC（顺时针），则线段OC的最小值为_____．

Answer 1

【答案】1

【解析】

连接OB，以OB为边作等边△BOE，根据等边三角形的性质可得BC=AB，OB=BE，∠ABC=∠EBO=60°，可得∠CBO=∠EBA，根据“SAS”可证△BCO≌△BAE，可得OC=AE，根据三角形的三边关系可得OC的最小值．

如图，连接OB，以OB为边作等边△BOE，

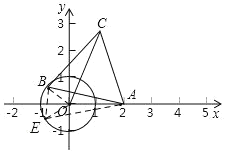
∵△ABC，△BOE都是等边三角形，

∴BC=AB,OB=BE,∠ABC=∠EBO=60°，

∴∠CBO=∠EBA，且BC=AB，BE=BO，

∴△BCO≌△BAE(SAS)

∴OC=AE，

在△AOE中，AE≥OE+AO，

∴当点E在线段AO时，AE的最小值为1，

∴OC的最小值为1，

故答案为：1