题目内容
【题目】如图,![]() 是
是![]() 的弦,过
的弦,过![]() 的中点
的中点![]() 作
作![]() ,垂足为
,垂足为![]() ,过点
,过点![]() 作直线
作直线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,使得
,使得![]() .
.
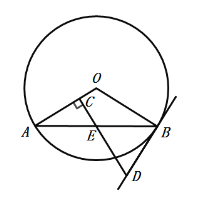
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的
的![]() 边上的高.
边上的高.
(3)在(2)的条件下,求![]() 的面积.
的面积.
【答案】(1)见解析;(2)4.5;(3)27
【解析】
(1)根据等腰三角形的性质可得![]() ,结合切线的判定方法可得结论;
,结合切线的判定方法可得结论;
(2)过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,结合中点及等腰三角形的性质可得
,结合中点及等腰三角形的性质可得![]() ,利用勾股定理可得DF的长;
,利用勾股定理可得DF的长;
(3)根据两组对应角分别相等的两个三角形相似可得![]() ,利用相似三角形对应线段成比例可求得EO长,由三角形面积公式求解即可.
,利用相似三角形对应线段成比例可求得EO长,由三角形面积公式求解即可.
(1)证明:∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]()
∴![]() ,
,
∴![]() ,
,
∴![]()
∵![]() 是圆的半径,
是圆的半径,
∴![]() 是
是![]() 的切线;
的切线;
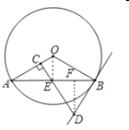
(2)如图,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,
,
∵点![]() 是
是![]() 的中点,
的中点,![]() ,
,
∴![]() ,
,![]() ,
,
又∵![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
(3)∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
由(2)得![]()
即![]() ,得
,得![]() ,
,
∴![]() 的面积是:
的面积是:![]() .
.

练习册系列答案
相关题目
【题目】随机抽取某小吃店一周的营业额(单位: 元)如下表:
星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 | 合计 |
|
|
|
|
|
|
|
(1)分析数据,填空:这组数据的平均数是 元,中位数是 元,众数是 元.
(2)估计一个月(按![]() 天计算)的营业额,星期一到星期五营业额相差不大,用这
天计算)的营业额,星期一到星期五营业额相差不大,用这![]() 天的平均数估算合适么?简要说明理由.
天的平均数估算合适么?简要说明理由.