Question

【题目】在平面直角坐标系xOy中，有任意三角形，当这个三角形的一条边上的中线等于这条边的一半时，称这个三角形叫“和谐三角形”，这条边叫“和谐边”，这条中线的长度叫“和谐距离”．

（1）已知A（2,0），B（0,4），C（1,2），D（4,1），这个点中，能与点O组成“和谐三角形”的点是 ，“和谐距离”是 ；

（2）连接BD，点M，N是BD上任意两个动点（点M，N不重合），点E是平面内任意一点，△EMN是以MN为“和谐边”的“和谐三角形”，求点E的横坐标t的取值范围；

（3）已知⊙O的半径为2，点P是⊙O上的一动点，点Q是平面内任意一点，△OPQ是“和谐三角形”，且“和谐距离”是2，请描述出点Q所在位置．

Answer 1

【答案】（1）A,B；；（2）；（3）点Q在以点O为圆心，4为半径的圆上；或在以点O为圆心，为半径的圆上．

【解析】

（1）由题意利用“和谐三角形”以及“和谐距离”的定义进行分析求解；

（2）由题意可知以BD的中点为圆心，以BD为直径作圆此时可求点E的横坐标t的取值范围；

（3）根据题意△OPQ是“和谐三角形”，且“和谐距离”是2，画出图像进行分析.

解：（1）由题意可知当A（2,0），B（0,4）与O构成三角形时满足圆周角定理即能与点O组成“和谐三角形”，此时“和谐距离”为；

（2）根据题意作图，以BD的中点为圆心，以BD为直径作圆，

可知当E在如图位置时求点E的横坐标t的取值范围，

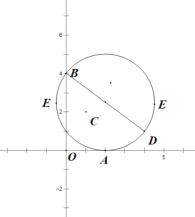
解得点E的横坐标t的取值范围为；

（3）如图

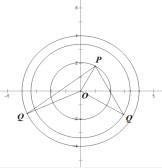
当PQ为“和谐边”时，点Q在以点O为圆心，为半径的圆上；

当OQ为“和谐边”时，点Q在以点O为圆心，4为半径的圆上.