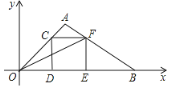
题目内容
【题目】若一个四位自然数满足个位与百位相同,十位与千位相同,我们称这个数为“双子数”.将“双子数”![]() 的百位、千位上的数字交换位置,个位、十位上的数字也交换位置,得到个新的双子数
的百位、千位上的数字交换位置,个位、十位上的数字也交换位置,得到个新的双子数![]() ,记
,记![]() 为“双子数”
为“双子数”![]() 的“双11数”.例如,
的“双11数”.例如,![]() ,
,![]() ,则
,则![]() .
.
(1)计算2424的“双11数”![]() ______;
______;
(2)若“双子数”![]() 的“双11数”的
的“双11数”的![]() 是一个完全平方数,求
是一个完全平方数,求![]() 的值;
的值;
(3)已知两个“双子数”![]() 、
、![]() ,其中
,其中![]() ,
,![]() (其中
(其中![]() ,
,![]() ,
,![]() ,
,![]() 且
且![]() 、
、![]() 、
、![]() 、
、![]() 都为整数,若
都为整数,若![]() 的“双11数”
的“双11数”![]() 能被17整除,且
能被17整除,且![]() 、
、![]() 的“双11数”满足
的“双11数”满足![]() ,令
,令![]() ,求
,求![]() 的值.
的值.
【答案】(1)12;(2)4或16或36;;(3)51或17.
【解析】
(1)直接根据“双子数”m的“双11数”的计算方法即可得出结论;
(2)设出四位数,进而得出F(m)=2(x+y),再求出0<x+y≤18,再根据F(m)是一个完全平方数,求出x+y,即可得出结论;
(3)先根据“双11数”F(p)能被17整除,进而判断出p为8989,求出F(q)=2(c+d),再根据F(p)+2F(q)﹣(4a+3b+2d+c)=0,得出d![]() ,进而求出c,d,即可得出结论.
,进而求出c,d,即可得出结论.
(1)由题意知,2424的“双11数”F(2424)![]() 12.
12.
故答案为:12;
(2)设“双子数”m的个位数字和十位数字分别为x,y,(0≤x≤9,0<y≤9)
则数字m为1000y+100x+10y+x=1010y+101x,
∴“双子数”m'为1010x+101y,
∴F(m)![]() 2(x+y).
2(x+y).
∵0≤x≤9,0<y≤9,
∴0<x+y≤18.
∵F(m)是一个完全平方数,
∴2(x+y)是一个完全平方数,
∴x+y=2或x+y=8或x+y=18,
∴F(m)=2×2=4或16或36,
即:F(m)的值为4或16或36;
(3)∵“双子数”p,p![]() ,
,
∴F(p)=2(a+b).
∵“双11数”F(p)能被17整除,
∴a+b是17的倍数.
∵1≤a<b≤9,
∴3≤a+b<18,
∴a+b=17,
∴a=8,b=9,
∴“双子数”p为8989,F(p)=34.
∵“双子数”q,q![]() ,
,
∴F(q)=2(c+d).
∵F(p)+2F(q)﹣(4a+3b+2d+c)=0,
∴34+2×2(c+d)﹣(4×8+3×9+2d+c)=0,
∴3c+2d=25,
∴d![]() ,
,
∵1≤c≤9,1≤d≤9,c≠d,c、d都为整数,
∴c为奇数,1≤c<9,
当c=1时,d=11,不符合题意,舍去,
当c=3时,d=8,
∴“双子数”q为3838,
∴G(p,q)![]() 51,
51,
当c=5时,d=5,不符合题意,舍去,
当c=7时,d=2,
∴“双子数”q为7272,
∴G(p,q)![]() 17,
17,
∴G(p,q)的值为51或17.

 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案