题目内容
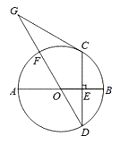
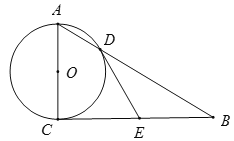
【题目】如图,已知⊙O的半径为1,AC是⊙O的直径,过点C作⊙O的切线BC,E是BC的中点,AB交⊙O于D点.
(1)直接写出ED和EC的数量关系:_________;
(2)DE是⊙O的切线吗?若是,给出证明;若不是,说明理由;
(3)填空:当BC=_______时,四边形AOED是平行四边形,同时以点O、D、E、C为顶点的四边形是_______.
【答案】ED=EC 2 正方形
【解析】
(1)连结CD,如图,由圆周角定理得到∠ADC=90°,然后根据直角三角形斜边上的中线直线得到DE=CE=BE;
(2)连结OD,如图,利用切线性质得∠2+∠4=90°,再利用等腰三角形的性质得∠1=∠2,∠3=∠4,所以∠1+∠3=∠2+∠4=90°,于是根据切线的判定定理可判断DE是⊙O 的切线;(3)要判断四边形AOED是平行四边形,则DE=OA=1,所以BC=2,当BC=2时,△ACB为等腰直角三角形,则∠B=45°,又可判断△BCD为等腰直角三角形,于是得到DE⊥BC,DE=![]() BC=1,所以四边形AOED是平行四边形;然后利用OD=OC=CE=DE=1,∠OCE=90°,可判断四边形OCED为正方形.
BC=1,所以四边形AOED是平行四边形;然后利用OD=OC=CE=DE=1,∠OCE=90°,可判断四边形OCED为正方形.
(1)连结CD,如图,
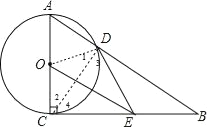
∵AC是⊙O的直径,
∴∠ADC=90°,
∵E是BC的中点,
∴DE=CE=BE;
(2)DE是⊙O的切线.理由如下:
连结OD,如图,
∵BC为切线,
∴OC⊥BC,
∴∠OCB=90°,即∠2+∠4=90°,
∵OC=OD,ED=EC,
∴∠1=∠2,∠3=∠4,
∴∠1+∠3=∠2+∠4=90°,即∠ODB=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
(3)当BC=2时,
∵CA=CB=2,
∴△ACB为等腰直角三角形,
∴∠B=45°,
∴△BCD为等腰直角三角形,
∴DE⊥BC,DE=![]() BC=1,
BC=1,
∵OA=DE=1,AO∥DE,
∴四边形AOED是平行四边形;
∵OD=OC=CE=DE=1,∠OCE=90°,
∴四边形OCED为正方形.
故答案为ED=EC;2,正方形.