题目内容
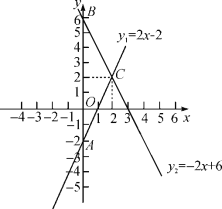
【题目】如图,已知点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,现将
,现将![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在第一象限的
落在第一象限的![]() 处,则直线
处,则直线![]() 与
与![]() 轴的交点
轴的交点![]() 的坐标为( )
的坐标为( )
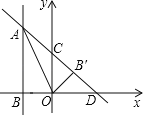
A.![]() B.
B.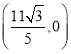 C.
C.![]() D.
D.![]()
【答案】D
【解析】
根据对称性得到∠BAO=∠CAO,由AB∥y轴得∠COA=∠BAO,可推出CA=CO,再根据勾股定理即可求得OC,进而求出直线AD解析式即可得结论.
根据翻折可知:
∠BAO=∠CAO,∠ABO=∠AB'O=90°,AB'=AB=9,OB'=OB=3.
∵AB⊥x轴,
∴AB∥y轴,
∴∠BAO=∠COA,
∴∠CAO=∠COA,
∴CA=CO,
设CA=x,则CO=x,CB'=9﹣x,
在Rt△OCB'中,根据勾股定理,得
OC2=OB'2+B'C2,即x2=32+(9﹣x)2,
解得:x=5,
∴OC=5,
∴C(0,5),
设直线AD解析式为y=kx+b,
将A(﹣3,9),C(0,5)代入,得
b=5,﹣3k+5=9,
解得:k![]() ,
,
∴直线AD解析式为y![]() x+5,
x+5,
当y=0时,x![]() ,
,
∴D点的坐标为(![]() ,0).
,0).
故选:D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】中秋节期间某水库养殖场为适应市场需求,连续用![]() 天时间,采用每天降低水位以减少捕捞成本的办法.对水库中某种鲜鱼进行捕捞销售,第
天时间,采用每天降低水位以减少捕捞成本的办法.对水库中某种鲜鱼进行捕捞销售,第![]() 天(
天(![]() 且
且![]() 为整数)的捕捞与销售的相关信息如下:
为整数)的捕捞与销售的相关信息如下:
鲜鱼销售单价(元 |
|
单位捕捞成本(元 |
|
捕捞量 |
|
假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出.
(1)求第![]() 天的收入
天的收入![]() (元)与
(元)与![]() (天)之间的函数关系式?(当天收入
(天)之间的函数关系式?(当天收入![]() 日销售额-日捕捞成本)
日销售额-日捕捞成本)
(2)在第几天![]() 取得最大值,最大值是多少?
取得最大值,最大值是多少?