题目内容
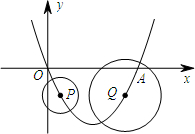
如图,抛物线y=
x2-
x与x轴交于O,A两点.半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动.两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动.设点P的横坐标为t.
(1)点Q的横坐标是______(用含t的代数式表示);
(2)若⊙P与⊙Q相离,则t的取值范围是______.
| 1 |
| 2 |
| 5 |
| 2 |
(1)点Q的横坐标是______(用含t的代数式表示);
(2)若⊙P与⊙Q相离,则t的取值范围是______.

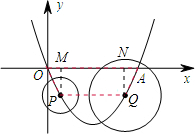
(1)连接OP、PQ、AQ.
∵抛物线y=
x2-
x与x轴交于O,A两点,
∴O与A关于抛物线的对称轴x=
对称,
又∵动圆(⊙P)的圆心从O点出发沿抛物线向靠近点A的方向移动;动圆(⊙Q)的圆心从A点出发沿抛物线向靠近点O的方向移动,两圆同时出发,且移动速度相等,
∴OP=AQ,P与Q也关于直线x=
对称,
∴四边形OPQA是等腰梯形.
作等腰梯形OPQA的高PM、QN,则OM=AN=t.
解方程
x2-
x=0,得x1=0,x2=5,
∴A(5,0),OA=5,
∴ON=OA-AN=5-t,
∴点Q的横坐标是5-t;
(2)若⊙P与⊙Q相离,分两种情况:
①⊙P与⊙Q外离,则PQ>2+1,即PQ>3.
∵OM=AN=t,OA=5,
∴PQ=MN=OA-OM-AN=5-2t,
∴5-2t>3,
解得t<1,
又∵t≥0,
∴0≤t<1;
②⊙P与⊙Q内含,则PQ<2-1,即PQ<1.
由①知PQ=5-2t,
∴5-2t<1,
解得t>2,
又∵两圆分别从O、A两点同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动,OA=5,点P的横坐标为t,
∴2t≤5,解得t≤
.
∴2<t≤
.
故答案为5-t;0≤t<1或2<t≤
.
∵抛物线y=
| 1 |
| 2 |
| 5 |
| 2 |
∴O与A关于抛物线的对称轴x=
| 5 |
| 2 |
又∵动圆(⊙P)的圆心从O点出发沿抛物线向靠近点A的方向移动;动圆(⊙Q)的圆心从A点出发沿抛物线向靠近点O的方向移动,两圆同时出发,且移动速度相等,
∴OP=AQ,P与Q也关于直线x=
| 5 |
| 2 |
∴四边形OPQA是等腰梯形.
作等腰梯形OPQA的高PM、QN,则OM=AN=t.
解方程
| 1 |
| 2 |
| 5 |
| 2 |
∴A(5,0),OA=5,
∴ON=OA-AN=5-t,
∴点Q的横坐标是5-t;
(2)若⊙P与⊙Q相离,分两种情况:
①⊙P与⊙Q外离,则PQ>2+1,即PQ>3.
∵OM=AN=t,OA=5,
∴PQ=MN=OA-OM-AN=5-2t,
∴5-2t>3,
解得t<1,
又∵t≥0,
∴0≤t<1;
②⊙P与⊙Q内含,则PQ<2-1,即PQ<1.
由①知PQ=5-2t,
∴5-2t<1,
解得t>2,
又∵两圆分别从O、A两点同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动,OA=5,点P的横坐标为t,
∴2t≤5,解得t≤
| 5 |
| 2 |
∴2<t≤
| 5 |
| 2 |
故答案为5-t;0≤t<1或2<t≤
| 5 |
| 2 |


练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目

 两点的抛物线的解析式.
两点的抛物线的解析式.