题目内容
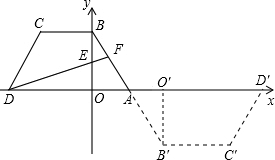
如图,在等腰梯形ABCD中,AD∥BC,BA=CD,AD的长为4,S梯形ABCD=9.已知点A、B的坐标分别为(1,0)和(0,3).
(1)求点C的坐标;
(2)取点E(0,1),连接DE并延长交AB于P试猜想DF与AB之间的关系,并证明你的结论;
(3)将梯形ABCD绕点A旋转180°后成梯形AB′C′D′,求对称轴为直线x=3,且过A、B′ 两点的抛物线的解析式.
两点的抛物线的解析式.
(1)求点C的坐标;
(2)取点E(0,1),连接DE并延长交AB于P试猜想DF与AB之间的关系,并证明你的结论;
(3)将梯形ABCD绕点A旋转180°后成梯形AB′C′D′,求对称轴为直线x=3,且过A、B′
 两点的抛物线的解析式.
两点的抛物线的解析式.(1)根据题意,点A、B的坐标分别为(1,0)和(0,3)易得OB=3,BC=2,
可得C到x轴的距离为3,到y轴的距离为2,
故C(-2,3).
(2)猜想:DF⊥AB.
根据题意,易得tan∠FDA=
=
,
同时可得tan∠BAO=-
=-3,
有tan∠FDA×tan∠BAO=-1,
故DF⊥AB.
(3)根据题意,设其方程为y=a(x-3)2+c,
同时有A(1,0),(5,0),
将其代入方程可得a=1,c=-4,
化简可得y=x2-6x+5,
故所求的抛物线解析式为y=x2-6x+5.
可得C到x轴的距离为3,到y轴的距离为2,
故C(-2,3).
(2)猜想:DF⊥AB.
根据题意,易得tan∠FDA=
| OE |
| OB |
| 1 |
| 3 |
同时可得tan∠BAO=-
| OB |
| OA |
有tan∠FDA×tan∠BAO=-1,
故DF⊥AB.
(3)根据题意,设其方程为y=a(x-3)2+c,
同时有A(1,0),(5,0),
将其代入方程可得a=1,c=-4,
化简可得y=x2-6x+5,
故所求的抛物线解析式为y=x2-6x+5.


练习册系列答案
相关题目
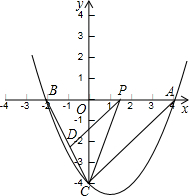

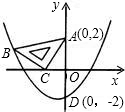 和点C,与抛物线y=ax2+ax+b交于点B,其中点A(0,2),点B(-3,1),抛物线与y轴交点D(0,-2).
和点C,与抛物线y=ax2+ax+b交于点B,其中点A(0,2),点B(-3,1),抛物线与y轴交点D(0,-2).