Question

已知：在平面直角坐标系xOy中，抛物线y=x²+bx+c经过A（1，1）、B（0，4）两点，M为抛物线的顶点．
（1）求这条抛物线的表达式及顶点M的坐标；
（2）设由（1）求得的抛物线的对称轴为直线l，点A关于直线l的对称点为点C，AC与直线l相交于点D，联结OD、OC．请直接写出C与D两点的坐标，并求∠COM+∠DOM的度数．

Answer 1

（1）由抛物线y=x²+bx+c经过A（1，1）、B（0，4）两点，
得

1+b+c=1 c=4.

解得

b=-4 c=4.

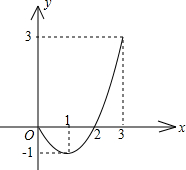
∴所求抛物线的表达式为y=x²-4x+4．
由y=x²-4x+4，得y=（x-2）²．
即得该抛物线的顶点M的坐标为（2，0）．

（2）由（1）得抛物线的对称轴是直线x=2．
根据题意，C与D两点的坐标分别是C（3，1）、D（2，1）．
设点D关于x轴的对称点为点E，连接OE，CE．
则点E的坐标为E（2，-1），且∠DOM=∠EOM．
利用两点间距离公式，
得OC=

32+12

=

10

，
OE=

22+(-1)2

=

5

，
CE=

(3-2)2+(1+1)2

=

5

．
∴OE=CE，OC²=10，OE²+CE²=5+5=10．
即得OE²+CE²=OC²．
∴∠OEC=90°
于是，由OE=CE，得∠COE=45°．
即得∠COM+∠DOM=∠COE=45°．