题目内容
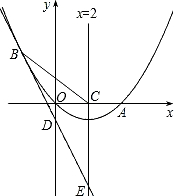
如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E.
(1)求m的值及该抛物线对应的函数关系式;
(2)求证:①CB=CE;②D是BE的中点;
(3)若P(x,y)是该抛物线上的一个动点,是否存在这样的点P,使得PB=PE?若存在,试求出所有符合条件的点P的坐标;若不存在,请说明理由.
(1)求m的值及该抛物线对应的函数关系式;
(2)求证:①CB=CE;②D是BE的中点;
(3)若P(x,y)是该抛物线上的一个动点,是否存在这样的点P,使得PB=PE?若存在,试求出所有符合条件的点P的坐标;若不存在,请说明理由.

(1)∵点B(-2,m)在直线y=-2x-1上
∴m=-2×(-2)-1=3
∴B(-2,3)
∵抛物线经过原点O和点A,对称轴为x=2
∴点A的坐标为(4,0)
设所求的抛物线对应函数关系式为y=a(x-0)(x-4)
将点B(-2,3)代入上式,得3=a(-2-0)(-2-4)
∴a=
∴所求的抛物线对应的函数关系式为y=
x(x-4)
即y=
x2-x;
(2)证明:①直线y=-2x-1与y轴、直线x=2的交点坐标分别为D(0,-1)E(2,-5),
过点B作BG∥x轴,与y轴交于F、直线x=2交于G,
则BG⊥直线x=2,BG=4
在Rt△BGC中,BC=
=5
∵CE=5,
∴CB=CE=5
②过点E作EH∥x轴,交y轴于H,
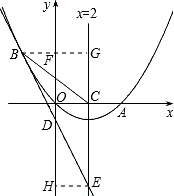
则点H的坐标为H(0,-5)
又点F、D的坐标为F(0,3)、D(0,-1)
∴FD=DH=4,BF=EH=2,∠BFD=∠EHD=90°
∴△DFB≌△DHE(SAS)
∴BD=DE
即D是BE的中点;
(3)存在.
由于PB=PE,∴点P在直线CD上
∴符合条件的点P是直线CD与该抛物线的交点
设直线CD对应的函数关系式为y=kx+b
将D(0,-1)C(2,0)代入,得
,
解得k=
,b=-1
∴直线CD对应的函数关系式为y=
x-1
∵动点P的坐标为(x,
x2-x)
∴
x-1=
x2-x
解得x1=3+
,x2=3-
∴y1=
,y2=
∴符合条件的点P的坐标为(3+
,
)或(3-
,
).
∴m=-2×(-2)-1=3
∴B(-2,3)
∵抛物线经过原点O和点A,对称轴为x=2
∴点A的坐标为(4,0)
设所求的抛物线对应函数关系式为y=a(x-0)(x-4)
将点B(-2,3)代入上式,得3=a(-2-0)(-2-4)
∴a=
| 1 |
| 4 |
∴所求的抛物线对应的函数关系式为y=
| 1 |
| 4 |
即y=
| 1 |
| 4 |
(2)证明:①直线y=-2x-1与y轴、直线x=2的交点坐标分别为D(0,-1)E(2,-5),
过点B作BG∥x轴,与y轴交于F、直线x=2交于G,
则BG⊥直线x=2,BG=4
在Rt△BGC中,BC=
| CG2+BG2 |
∵CE=5,
∴CB=CE=5
②过点E作EH∥x轴,交y轴于H,

则点H的坐标为H(0,-5)
又点F、D的坐标为F(0,3)、D(0,-1)
∴FD=DH=4,BF=EH=2,∠BFD=∠EHD=90°
∴△DFB≌△DHE(SAS)
∴BD=DE
即D是BE的中点;
(3)存在.
由于PB=PE,∴点P在直线CD上
∴符合条件的点P是直线CD与该抛物线的交点
设直线CD对应的函数关系式为y=kx+b
将D(0,-1)C(2,0)代入,得
|
解得k=
| 1 |
| 2 |
∴直线CD对应的函数关系式为y=
| 1 |
| 2 |
∵动点P的坐标为(x,
| 1 |
| 4 |
∴
| 1 |
| 2 |
| 1 |
| 4 |
解得x1=3+
| 5 |
| 5 |
∴y1=
1+
| ||
| 2 |
1-
| ||
| 2 |
∴符合条件的点P的坐标为(3+
| 5 |
1+
| ||
| 2 |
| 5 |
1-
| ||
| 2 |

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
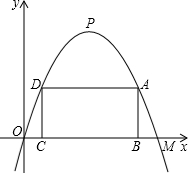 、M两点,OM=4;矩形ABCD的边BC在线段的OM上,点A、D在抛物线上.
、M两点,OM=4;矩形ABCD的边BC在线段的OM上,点A、D在抛物线上.