��Ŀ����
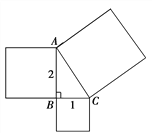
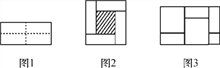
����Ŀ����ͼ1��һ����Ϊ2m����Ϊ2n�ij���������ͼ�������ü���ƽ���ֳ�4��С��������Ȼ��ͼ2����״ƴ��һ�������Σ�
(1)ͼ2����Ӱ���ֵ����Ϊ ��
(2)�۲�ͼ2������д��ʽ��(m��n)2��(m��n)2��mn֮��ĵ�����ϵ�� ��
(3)��x��y����6��xy��2.75����x��y�� ��
(4)ʵ������������ʽ������ͼ�ε��������ʾ����ͼ3������ʾ��ʽ�� ��
���𰸡���1��(m��n)����2��(m��n)��(m��n)��4mn����3����5����4��(2a��b)(a��b)��2a��3ab��b��
�����������������
�����������1�����þ��������ʽ����.(2)���ݾ��������ʽ�ɵõ�m,n��ϵ.(3)���ã�2���Ĺ�ʽ����.(4)���ݾ��������ʽ�ֱ������巽���Ͳ��ֵĺ͵ķ����е�ʽ.
���������
(1)ͼ2����Ӱ���ֵı߳���m-n,���Ϊ(m��n)2��
(2)�۲�ͼ2������д��ʽ��(m��n)2��(m��n)2��mn֮��ĵ�����ϵ���������������(m��n)2 ����Ӱ���������(m��n)2 ���ĸ����������4mn ������(m��n)2��(m��n)2��4mn��
(3)��Ϊx��y����6��xy��2.75�����ù�ʽ(m��n)2��(m��n)2��4mn����![]() +
+![]() ,���x��y����5.
,���x��y����5.
(4)ʵ������������ʽ������ͼ�ε��������ʾ����ͼ3���ֱ���ÿ��С����ͼ�ε�������2a2��3ab��b2�����������(2a��b)(a��b)��
����ʾ��ʽ��(2a��b)(a��b)��2a2��3ab��b2��