题目内容
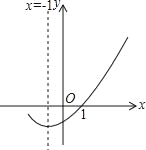
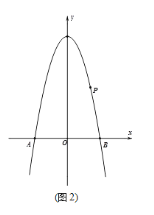
【题目】如图,抛物线y=ax2-4n+4经过点P(2,4),与x轴交于A、B两点,过点P作直线l∥x轴,点C为第二象限内直线l上方,抛物线上一个动点,其横坐标为m。
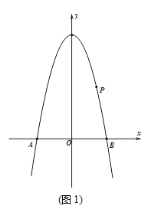

(1)如图(1),若AB=6, 求抛物线解析式
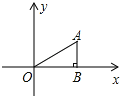
(2)如图(2),在(1)的条件下,设点C的横坐标为t,ACP的面积S,求S与t之间的函数关系式.
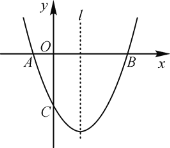
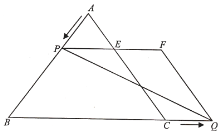
(3)如图(3),连接OP,过点C作EC∥OP交抛物线于点E,直线PE、CP分别交x轴于点G、H,当PG=PH时,求a的值。
【答案】(1)y=-![]() x+
x+ ![]() ;(2)S=
;(2)S=![]() ;(3)a=-
;(3)a=-![]()
【解析】
(1)根据题意可得A(-3,0),然后将点A、P的坐标代入抛物线解析式求出a和n即可;
(2)首先求出直线AP的解析式,然后过点C作y轴的平行线交直线AP于点M,根据点C的横坐标为t可表示出C、M的坐标,求出CM的长,再利用三角形面积公式计算即可;
(3)根据PG=PH可得∠PGH=∠PHG,设直线PG解析式为:y-4=k(x-2),则直线PH解析式为:y-4=-k(x-2),分别联立直线解析式和抛物线解析式求出E(![]() ,
,![]() ),C(
),C(![]() ,
,![]() ),然后根据EC∥OP列方程求解即可.
),然后根据EC∥OP列方程求解即可.
解:(1)∵抛物线对称轴为x=0,AB=6,
∴A(-3,0),B(3,0),
将A(-3,0),P(2,4)代入y=ax2-4n+4得:![]() ,
,
解得: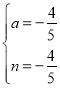 ,
,
∴抛物线解析式为:![]() ;
;
(2)设直线AP的解析式为:y=kx+b(k≠0),
将A(-3,0),P(2,4)代入得:![]() ,
,
解得: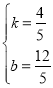 ,
,
∴直线AP的解析式为:![]() ,
,
如图,过点C作y轴的平行线交直线AP于点M,则C(t,![]() ),M(t,
),M(t,![]() ),
),
∴![]() ,
,
∴![]() ;
;
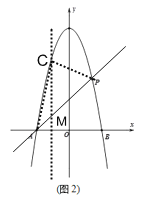
(3)将点P(2,4)代入抛物线y=ax2-4n+4得:4=4a-4n+4,
∴n=a,即抛物线解析式为:y=ax2-4a+4,
∵PG=PH,
∴∠PGH=∠PHG,
设直线PG解析式为:y-4=k(x-2),则直线PH解析式为:y-4=-k(x-2),
联立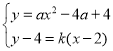 ,解得:
,解得: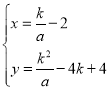 或
或![]() (舍去),
(舍去),
∴E点坐标为:(![]() ,
,![]() ),
),
同理,联立直线PH解析式和抛物线解析式可得:C(![]() ,
,![]() ),
),
易得直线OP解析式为:y=2x,
∵EC∥OP,
∴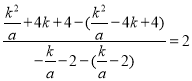 ,
,
解得:![]() .
.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案【题目】某中学开展“头脑风暴”知识竞赛活动,八年级![]() 班和
班和![]() 班各选出
班各选出![]() 名选手参加初赛,两个班的选手的初赛成绩(单位:分)分别是:
名选手参加初赛,两个班的选手的初赛成绩(单位:分)分别是:
1班85 80 75 85 100
2班80 100 85 80 80
(1)根据所给信息将下面的表格补充完整;
平均数 | 中位数 | 众数 | 方差 | |
|
|
| ||
|
|
|
(2)根据问题(1)中的数据,判断哪个班的初赛成绩较为稳定,并说明理由.