题目内容
【题目】如图,一次函数y=kx+b的图象与二次函数y=﹣x2+c的图象相交于A(﹣1,2),B(2,n)两点.
(1)求一次函数和二次函数的解析式;
(2)根据图象直接写出使二次函数的值大于一次函数的值的x的取值范围;
(3)设二次函数y=﹣x2+c的图象与y轴相交于点C,连接AC,BC,求△ABC的面积.
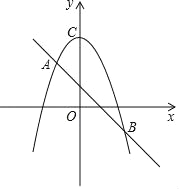
【答案】(1)y=﹣x+1;(2)﹣1<x<2;(3)3;
【解析】
(1)根据待定系数法求一次函数和二次函数的解析式即可.
(2)根据图象以及点A,B两点的坐标即可求出使二次函数的值大于一次函数的值的x的取值范围;
(3)连接AC、BC,设直线AB交y轴于点D,根据![]() 即可求出△ABC的面积.
即可求出△ABC的面积.
(1)把A(﹣1,2)代入y=﹣x2+c得:﹣1+c=2,
解得:c=3,
∴y=﹣x2+3,
把B(2,n)代入y=﹣x2+3得:n=﹣1,
∴B(2,﹣1),
把A(﹣1,2)、B(2,﹣1)分别代入y=kx+b得![]()
解得: ![]()
∴y=﹣x+1;
(2)根据图象得:使二次函数的值大于一次函数的值的x的取值范围是﹣1<x<2;
(3)连接AC、BC,设直线AB交y轴于点D,
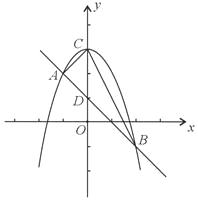
把x=0代入y=﹣x2+3得:y=3,
∴C(0,3),
把x=0代入y=﹣x+1得:y=1,
∴D(0,1),
∴CD=3﹣1=2,
则![]()

练习册系列答案
相关题目
【题目】某商场用5500元购进甲、乙两种矿泉水共180箱,矿泉水的成本价与销售价如下表所示:
类别 | 成本价(元 | 销售价(元 |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这180箱矿泉水,可获利多少元?