题目内容
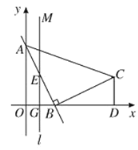
【题目】如图,在一面靠墙(墙的最大可用长度为8 m)的空地上用长为24 m的篱笆围成中间隔有二道篱笆的长方形花圃.设花圃的宽AB为x m,面积为S m2.
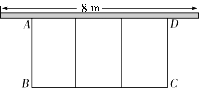
(1)求S关于x的函数关系式及自变量的取值范围;
(2)求所围成花圃的最大面积.
【答案】(1)S=4x2+24x,自变量的取值范围为:4≤x≤6.(2)32m2.
【解析】
(1)根据AB为xm,BC就为(24-4x)m,利用长方形的面积公式,可求出关系式.
(2)由(1)可知S和x为二次函数关系,根据二次函数的性质即可求围成的长方形花圃的最大面积.
(1)∵花圃的宽AB为x m,
∴花圃的长BC为24-4x m,
∴S=(24-4x)·x=4x2+24x,
∵![]() ,
,
解得:4≤x≤6,
∴S关于x的函数关系式为:S=4x2+24x,自变量的取值范围为:4≤x≤6.
(2)解:由(1)知S=4x2+24x(4≤x≤6),
∴S=4(x-3)x2+36,
由函数性质可知:当x>3时,y随x的增大而减少,
∴当x=4时,Smax=32(m2).
答:所围成花圃的最大面积为32m2.

练习册系列答案
相关题目
【题目】A,B两地相距20km.甲、乙两人都由A地去B地,甲骑自行车,平均速度为10km/h;乙乘汽车,平均速度为40km/h,且比甲晚1.5h出发.设甲的骑行时间为x(h)(0≤x≤2)
(1)根据题意,填写下表:
时间x(h) 与A地的距离 | 0.5 | 1.8 | _____ |
甲与A地的距离(km) | 5 |
| 20 |
乙与A地的距离(km) | 0 | 12 |
|
(2)设甲,乙两人与A地的距离为y1(km)和y2(km),写出y1,y2关于x的函数解析式;
(3)设甲,乙两人之间的距离为y,当y=12时,求x的值.