题目内容
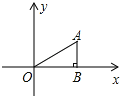
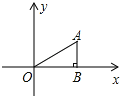
【题目】如图,△ABC中,∠ABC=90°
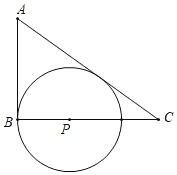
(1)在BC边上找一点P,作⊙P与AC,AB边都相切,与AC的切点为Q;(尺规作图,保留作图痕迹)
(2)若AB=4,AC=6,求第(1)题中所作圆的半径;
(3)连接BQ,第(2)题中的条件不变,求cos∠CBQ的值.
【答案】(1)见解析;(2)r=![]() ;(3)
;(3)![]()
【解析】
(1)作∠BAC的平分线交BC于点P,作PQ⊥AC于Q,以P为圆心,PQ为半径作⊙P即可.
(2)利用面积法求解即可.
(3)证明∠CBQ=∠BAP,可得cos∠CBQ=cos∠BAP=![]() ,由此计算即可.
,由此计算即可.
解:(1)如图,⊙P即为所求.
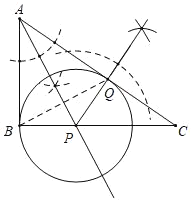
(2)在Rt△ABC中,∵AB=4,AC=6,
∴BC=![]() =2
=2![]() ,
,
∵PA平分∠BAC,PB⊥BA,PQ⊥AC,
∴PB=PQ,设PB=PQ=r,
∵S△ABC=S△ABP+S△ACP,
∴![]() ×4×2
×4×2![]() =
=![]() ×4×r+
×4×r+![]() ×6×r,
×6×r,
∴r=![]() .
.
(3)∵∠ABP=∠AQP=90°,AP=AP,PB=PQ,
∴Rt△APB≌Rt△APQ(HL),
∴AB=AQ,∵PB=PQ,
∴PA垂直平分线段BQ,
∴∠CBQ+∠ABQ=90°,∠BAP+∠APB=90°,
∴∠CBQ=∠BAP,
∴cos∠CBQ=cos∠BAP=![]() =
=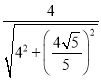 =
=![]() .
.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目