题目内容
【题目】正方形![]() 中,
中,![]() 是
是![]() 中点,点
中点,点![]() 从点
从点![]() 出发沿
出发沿![]() 的路线匀速运动,到点
的路线匀速运动,到点![]() 停止,点
停止,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 路线匀速运动,
路线匀速运动,![]() 、
、![]() 两点同时出发,点
两点同时出发,点![]() 的速度是点
的速度是点![]() 速度的
速度的![]() 倍
倍![]() ,当点
,当点![]() 停止时,点
停止时,点![]() 也同时停止运动,设
也同时停止运动,设![]() 秒时,正方形
秒时,正方形![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,
,![]() 关于
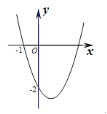
关于![]() 的函数关系如图2所示,则
的函数关系如图2所示,则
(1)求正方形边长![]() ;
;
(2)求![]() 的值;
的值;
(3)求图2中线段![]() 所在直线的解析式.
所在直线的解析式.
【答案】(1)AB=12;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)当t=0时,y=144-AB2,即可求解;
(2)y=S正方形AECD-S△APM-S△DQM得:y=144-3t-3mt,将点K(4,96)代入上式,即可求解;
(3)当4<t≤8时,y=S正方形ABCD-S梯形ABPM-S△DQM =180-21t,求得点E(8,12),同理可得点F(9,0),即可求解
(1)当![]() 时,
时,![]() ,
,
解得:AB=12;
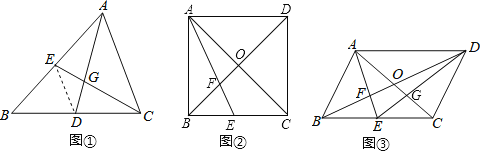
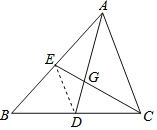
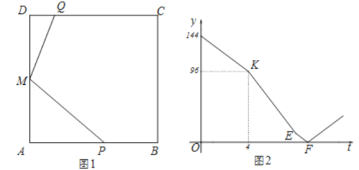
(2)当0≤t≤4时,如图1所示,
![]()
即:![]() ,
,
将点K(4,96)代入上式并解得:![]() ;
;
(3)当![]() 时,
时,
此时,点P在BC上,点Q在CD上,如下图2所示:
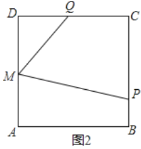
![]() ,
,
当![]() 时,
时,![]() ,
,
故点E(8,12),
同理可得点F(9,0),
将点E、F的坐标代入一次函数表达式:![]() 得:
得:![]() ,解得:
,解得:![]() ,
,
故线段EF所在直线的解析式为:![]() .
.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目