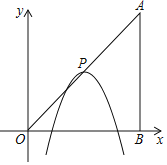题目内容
【题目】已知抛物线![]() 过点(3,1),D为抛物线的顶点.直线l:
过点(3,1),D为抛物线的顶点.直线l:![]() 经过定点A.
经过定点A.
(1)直接写出抛物线的解析式和点A的坐标;
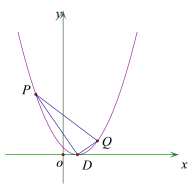
(2)如图,直线l与抛物线交于P,Q两点.
①求证:∠PDQ=90°;
②求△PDQ面积的最小值.
【答案】(1)抛物线解析式为![]() ;A(1,4)(2)①证明见解析;②当
;A(1,4)(2)①证明见解析;②当![]() 时,
时,![]() 取得最小值16.
取得最小值16.
【解析】
(1)将点![]() 代入解析式求得
代入解析式求得![]() 的值即可;直线l:
的值即可;直线l:![]() 经过定点A.
经过定点A.
即此时取值与K无关,即![]() =
=![]() 中K系数为0,即可求出点A坐标。
中K系数为0,即可求出点A坐标。
(2)①设点![]() 的坐标为
的坐标为![]() ,
,![]() ,点
,点![]() 为
为![]() ,
,![]() ,联立直线和抛物线解析式,化为关于
,联立直线和抛物线解析式,化为关于![]() 的方程可得
的方程可得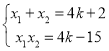 ,据此知
,据此知![]() ,由
,由![]() 、
、![]() 、
、![]() 、
、![]() 知
知![]() ,即
,即![]() ,从而得
,从而得![]() ,据此进一步求解可得;
,据此进一步求解可得;
②过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,则
,则![]() ,根据
,根据![]() 列出关于
列出关于![]() 的等式求解可得.
的等式求解可得.
解:(1)将点![]() 代入解析式,得:
代入解析式,得:![]() ,
,
解得:![]() ,
,
所以抛物线解析式为![]() ;
;
∵直线l:![]() 经过定点A.
经过定点A.
∴![]() =
=![]() 中当x=1时,y=4,
中当x=1时,y=4,
∴定点A为(1,4).
(2)①证明:设点![]() 的坐标为
的坐标为![]() ,
,![]() ,点
,点![]() 为
为![]() ,
,![]() ,(其中
,(其中![]() ,
,![]() ,
,![]() ,
,
由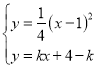 ,得:
,得:![]() ,
,
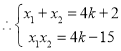 ,
,
![]() ,
,
如图2,分别过点![]() 、
、![]() 作
作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() 、
、![]() ,
,
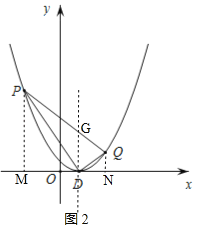
则![]() ,
,![]() ,
,
![]() 、
、![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
而![]() ,
,
![]() ,即
,即![]() ;
;
②过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,
,
所以![]() ,
,
![]() ,
,
![]() 当
当![]() 时,
时,![]() 取得最小值16.
取得最小值16.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目