��Ŀ����
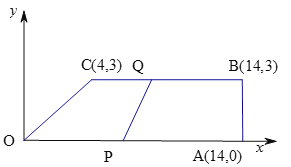
����Ŀ����ͼ������OABC�У�OΪֱ������ϵ��ԭ�㣬A��B��C������ֱ�Ϊ(14��0)��(14��3)��(4��3).��P��Qͬʱ��ԭ��������ֱ��������˶�����P��OA��ÿ��1����λ���յ�A�˶�����Q��OC��CB��ÿ��2����λ���յ�B�˶�.������������һ�㵽���Լ����յ�ʱ����һ��Ҳֹͣ�˶�.
(1)��ӳ������˶���x�룬��x>2.5ʱ��Q������ꣻ
(2)��x���ڶ���ʱ���ı���OPQCΪƽ���ı��Σ�
���𰸡���1��Q��2x��1��3������2��5��
��������
��1�����ȵó�Q���˶��ľ��������ʾ��Q�����꼴�ɣ�
��2������ƽ���ı��ε����ʵó�QC=OP�����ɵó��𰸣�
��1������������㵽�յ���Ҫ��ʱ�䣺
��C��4��3������OC![]() 5��
5��
��B��14��3������BC=14��4=10��
�������֪����x��2.5ʱ��Q����CB���˶����ʺ�����Ϊ��2x��5+4=2x��1��������Ϊ3����Q������Ϊ����2x��1��3����
��2����C��4��3����B��14��3������CB��OA����CQ��OP����CQ=OPʱ���ı���OPQCΪƽ���ı��Σ���2x��5=x����ã�x=5��
�𣺵�x=5ʱ���ı���OPQCΪƽ���ı��Σ�

��ϰ��ϵ�д�
�����Ŀ