题目内容
【题目】如图，四边形AOBC和四边形CDEF都是正方形，边OA在x轴上，边OB在y轴上，点D在边CB上，反比例函数y= 
在第二象限的图象经过点E，则正方形AOBC和正方形CDEF的面积之差为（ ）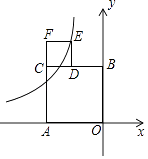
A.12
B.10
C.8
D.6
【答案】C
【解析】解：设正方形AOBC的边长为a，正方形CDEF的边长为b，则E（a﹣b，a+b），
∴（a+b）（a﹣b）=8，
整理为a2﹣b2=8，
∵S正方形AOBC=a2，S正方形CDEF=b2，
∴S正方形AOBC﹣S正方形CDEF=8，
所以答案是：C．
【考点精析】根据题目的已知条件，利用比例系数k的几何意义和正方形的性质的相关知识可以得到问题的答案，需要掌握几何意义：表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积；正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．
练习册系列答案
相关题目
