题目内容
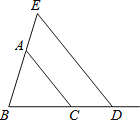
【题目】如图,在△ABC中,AD,AE,AF分别为△ABC的高线、角平分线和中线.

(1)写出图中所有相等的角和相等的线段;
(2)当BF=8cm,AD=7 cm时,求△ABC的面积.
【答案】(1)∠BAE=∠CAE,∠ADC=∠ADB,BF=FC;(2)56cm![]()
【解析】
(1)分别根据角平分线定义、三角形的高线和三角形的中线定义解决问题即可;
(2)根据三角形的面积公式列式求解即可.
解:(1)∵AE是△ABC的角平分线,
∴∠BAE=∠CAE.
∵AD是△ABC的高,
∴∠ADB=∠ADC=90°.
∵AF是△ABC的中线,
∴BF=CF.
图中所有相等的角和相等的线段为:∠BAE=∠CAE,∠ADB=∠ADC=90°,BF=CF.
(2)∵BF=CF,BF=8cm,AD=7cm,
∴BC=2BF=2×8=16cm,
∴S△ABC=![]() BCAD=
BCAD=![]() ×16cm×7cm
×16cm×7cm
=56cm2.
答:△ABC的面积是56cm2.

练习册系列答案
相关题目