题目内容
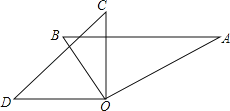
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内的一点,PA=3,PB=1,CD=PC=2,CD⊥PC.
(1)找出图中一对全等三角形,并证明;
(2)求∠BPC的度数.

【答案】(1)△APC≌△BDC,理由见解析;(2) ∠BPC=135°.
【解析】
(1)根据同角的余角相等求出∠ACP=∠BCD,再利用“边角边”证明△APC≌△BDC;
(2)先判断出△PCD是等腰直角三角形,再根据全等三角形对应边相等可得AP=BD,然后利用勾股定理逆定理判断出△BPD是直角三角形,∠BPD=90°,再根据∠BPC=∠BPD+∠CPD代入数据计算即可得解
(1)△APC≌△BDC,理由如下:
∵∠ACB=90°,CD⊥CP,∴∠ACB=∠PCD,
∴∠ACB-∠PCB=∠PCD-∠PCB,
即∠ACP=∠BCD,
又∵AC=BC,PC=DC,∴△APC≌△BDC(SAS).
(2)∵△APC≌△BDC,∴AP=BD,
∵PC=CD=2,∠PCD=90°,
∴PD2=PC2+CD2=8,∠CPD=45°.
∵PA=3,PB=1,∴BD=3,∴BD2=9,PB2=1.
∴BD2=PB2+PD2,∴∠BPD=90°.
∴∠BPC=∠BPD+∠CPD=135°.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目