题目内容
【题目】在△ABC中,∠ACB=90°,经过点B的直线l(不与直线AB重合)与直线BC的夹角等于∠ABC,分别过点C、点A作直线l的垂线,垂足分别为点D、点E.
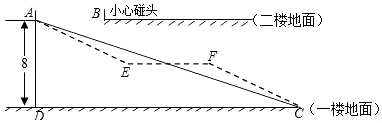
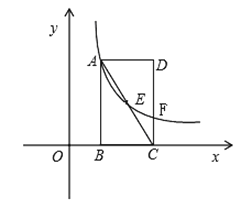
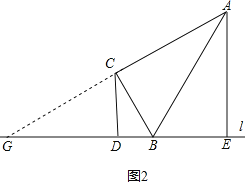
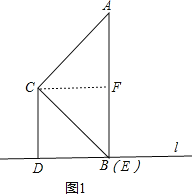
(1)如图1,当点E与点B重合时,若AE=4,判断以C点为圆心CD长为半径的圆C与直线AB的位置关系并说明理由;
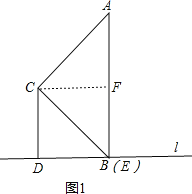
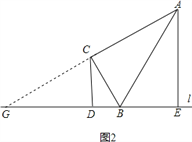
(2)如图2,当点E在DB延长线上时,求证:AE=2CD;
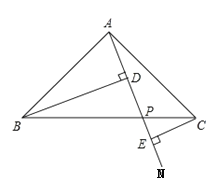
(3)记直线CE与直线AB相交于点F,若,![]() ,CD=4,求BD的长.
,CD=4,求BD的长.
【答案】(1)以C点为圆心CD长为半径的圆C与直线AB的位置关系是相切 (2)证明见解析(3) BD的长为2或8.
【解析】分析:
(1)如图1,过点C作CF⊥AB于点F,由已知条件易证此时四边形DBFC是正方形,由此可得CF=CD,从而可得此时以点C为圆心,CD长为半径的圆C与直线AB的位置关系是相切;
(2)如图2,延长AC交直线l于点G,由∠ACB=90°,∠ABC=∠GBC结合“三角形内角和定理”可得∠BAC=∠BGC,由此可得AB=GB,结合BC⊥AG可得AC=GC,由CD⊥l,AE⊥l可得CD∥AE,由此即可得到CD:AE=GC:GA=1:2,从而可得结论AE=2CD;
(3)如图3和图4,分点E在线段DB的延长线上和线段DB上两种情况作出符合要求的图形,并过点C作CG∥l交AB于点H,交AE于点G,然后结合已知条件和(2)中所得结论进行分析计算即可.
详解:
(1)以C点为圆心CD长为半径的圆C与直线AB的位置关系是相切,
理由如下:
如图1,过点C作CF⊥AB,垂足为点F,
∵CD⊥l,AB⊥l,CF⊥AB,
∴∠CDB=∠DBA=∠CFB=90°,
∴四边形DBFC是矩形,
∵∠ABD=90°,∠ABC=∠CBD,
∴ ∠ABC=∠CBD=45°,
∵∠ACB=90°,∠ABC=45°,
∴ ∠BCF=∠ABC=45°,
∴CF=BF,
∴四边形DBFC是正方形,
∴CF=CD=2,
∴圆C与直线AB相切;
(2)如图2,延长AC交直线l于点G,
∵∠ACB=90°,∠ABC=∠GBC
∴∠BAC=∠BGC
∴ AB=GB
∴ AC=GC,
∵ AE⊥l,CD⊥l,
∴ AE∥CD
∴ ![]() ,
,
∴AE=2CD
(3)由题意分以下两种情况解答:
(I)如图3,当点E在DB延长线上时:
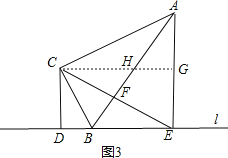
过点C作CG∥l交AB于点H,交AE于点G,则∠CBD=∠HCB,
∵∠ABC=∠CBD,
∴∠ABC=∠HCB,
∴CH=BH,
∵∠ACB=90°,
∴∠ABC+∠BAC=∠HCB+∠HCA=90°
∴∠BAC=∠HCA
∴CH=AH=BH,
∵CG∥l,
∴![]() ,
,
设CH=5x,则BE=6x,AB=10x
在Rt△ABE中,![]()
由(2)知AE=2CD=8,
∴8x=8,得x=1
∴CH=5,BE=6,AB=10
∵ CG∥l,
∴ ![]() ,
,
∴HG=3,
∴CG=CH+HG=8,
∵四边形CDEG是矩形,
∴DE=CG=8
∴BD=DE-BE=2;
(Π)如图4,当点E在DB上时:
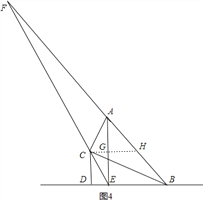
同理可得CH=5,BE=6,HG=3,
∴DE=CG=GH-HG=2
∴BD=DE+BE=8,
综上所述,BD的长为2或8.