ΧβΡΩΡΎ»ί
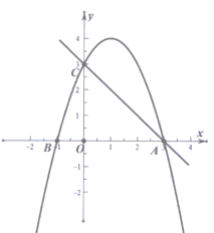
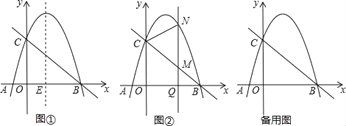
ΓΨΧβΡΩΓΩ»γΆΦΔΌ“―÷Σ≈ΉΈοœΏy=ax2©¹3ax©¹4aΘ®aΘΦ0Θ©ΒΡΆΦœσ”κx÷αΫΜ”ΎAΓΔBΝΫΒψΘ®A‘ΎBΒΡΉσ≤ύΘ©Θ§”κyΒΡ’ΐΑκ÷αΫΜ”ΎΒψCΘ§Ν§ΫαBCΘ§Εΰ¥ΈΚ· ΐΒΡΕ‘≥Τ÷α”κx÷αΒΡΫΜΒψΈΣEΘ°
Θ®1Θ©≈ΉΈοœΏΒΡΕ‘≥Τ÷α”κx÷αΒΡΫΜΒψEΉχ±ξΈΣ_____Θ§ΒψAΒΡΉχ±ξΈΣ_____ΘΜ
Θ®2Θ©»τ“‘EΈΣ‘≤–ΡΒΡ‘≤”κy÷αΚΆ÷±œΏBCΕΦœύ«–Θ§ ‘«σ≥ω≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§»γΆΦΔΎQΘ®mΘ§0Θ© «xΒΡ’ΐΑκ÷α…œ“ΜΒψΘ§ΙΐΒψQΉςy÷αΒΡΤΫ––œΏΘ§”κ÷±œΏBCΫΜ”ΎΒψMΘ§”κ≈ΉΈοœΏΫΜ”ΎΒψNΘ§Ν§ΫαCNΘ§ΫΪΓςCMN―ΊCNΖ≠’έΘ§MΒΡΕ‘”ΠΒψΈΣMΓδΘ°‘ΎΆΦΔΎ÷–ΧΫΨΩΘΚ «Ζώ¥φ‘ΎΒψQΘ§ ΙΒΟMΓδ«ΓΚΟ¬δ‘Ύy÷α…œΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ωQΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©(1.5Θ§0) (-1Θ§0)
Θ®2Θ©![]() ΘΜ
ΘΜ
Θ®3Θ©¥φ‘ΎΘ§![]() .
.
ΓΨΫβΈωΓΩ
Θ®1Θ©”…≈ΉΈοœΏ![]() ΒΡΕ‘≥Τ÷αΈΣ÷±œΏ
ΒΡΕ‘≥Τ÷αΈΣ÷±œΏ![]() «σ≥ω≈ΉΈοœΏy=ax2©¹3ax©¹4aΘ®aΘΦ0Θ©ΒΡΕ‘≥Τ÷αΖΫ≥ΧΘ§Φ¥Ω…«σΒΟΒψEΒΡΉχ±ξΘΜ‘Ύy=ax2©¹3ax©¹4aΘ®aΘΦ0Θ©Ννy=0Ω…ΒΟΙΊ”ΎxΒΡΖΫ≥Χax2©¹3ax©¹4a=0Θ§ΫβΖΫ≥ΧΦ¥Ω…«σΒΟΒψAΒΡΉχ±ξΘΜ
«σ≥ω≈ΉΈοœΏy=ax2©¹3ax©¹4aΘ®aΘΦ0Θ©ΒΡΕ‘≥Τ÷αΖΫ≥ΧΘ§Φ¥Ω…«σΒΟΒψEΒΡΉχ±ξΘΜ‘Ύy=ax2©¹3ax©¹4aΘ®aΘΦ0Θ©Ννy=0Ω…ΒΟΙΊ”ΎxΒΡΖΫ≥Χax2©¹3ax©¹4a=0Θ§ΫβΖΫ≥ΧΦ¥Ω…«σΒΟΒψAΒΡΉχ±ξΘΜ
Θ®2Θ©»γΆΦ1Θ§…ηΓ―E”κ÷±œΏBCœύ«–”ΎΒψDΘ§Ν§Ϋ”DEΘ§‘ρDEΓΆBCΘ§ΫαΚœΘ®1Θ©Ω…ΒΟDE=OE=![]() Θ§EB=
Θ§EB=![]() Θ§OC=-4aΘ§‘ΎRtΓςBDE÷–”…Ι¥Ι…Ε®άμΩ…ΒΟBD=2Θ§’β―υ”…tanΓœOBC=
Θ§OC=-4aΘ§‘ΎRtΓςBDE÷–”…Ι¥Ι…Ε®άμΩ…ΒΟBD=2Θ§’β―υ”…tanΓœOBC=![]() Φ¥Ω…Ν–≥ωΙΊ”ΎaΒΡΖΫ≥ΧΘ§ΫβΖΫ≥Χ«σΒΟaΒΡ÷ΒΦ¥Ω…ΒΟΒΫ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Φ¥Ω…Ν–≥ωΙΊ”ΎaΒΡΖΫ≥ΧΘ§ΫβΖΫ≥Χ«σΒΟaΒΡ÷ΒΦ¥Ω…ΒΟΒΫ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®3Θ©”…’έΒΰΒΡ–‘÷ ΚΆMNΓΈy÷αΩ…ΒΟΓœMCN=ΓœMΓδCN=ΓœMNCΘ§”…¥ΥΩ…ΒΟCM=MNΘ§”…ΒψBΒΡΉχ±ξΈΣΘ®4Θ§0Θ©Θ§ΒψCΒΡΉχ±ξΈΣΘ®0Θ§3Θ©Ω…ΒΟœΏΕΈBC=5Θ§÷±œΏBCΒΡΫβΈω ΫΈΣy=©¹![]() x+3Θ§”…¥ΥΦ¥Ω…ΒΟΒΫMΓΔNΒΡΉχ±ξΖ÷±πΈΣΘ®mΘ§©¹
x+3Θ§”…¥ΥΦ¥Ω…ΒΟΒΫMΓΔNΒΡΉχ±ξΖ÷±πΈΣΘ®mΘ§©¹![]() m+3Θ©ΓΔΘ®mΘ§©¹
m+3Θ©ΓΔΘ®mΘ§©¹![]() m2+
m2+![]() m+3Θ©Θ§ΉςMFΓΆOC”ΎFΘ§’β―υ”…sinΓœBCO=
m+3Θ©Θ§ΉςMFΓΆOC”ΎFΘ§’β―υ”…sinΓœBCO=![]() Φ¥Ω…ΫβΒΟCM=
Φ¥Ω…ΫβΒΟCM=![]() mΘ§»ΜΚσΖ÷ΒψN‘Ύ÷±œΏBCΒΡ…œΖΫΚΆœ¬ΖΫΝΫ÷÷«ιΩω”ΟΚ§mΒΡ¥ζ ΐ Ϋ±μ¥ο≥ωMNΒΡ≥ΛΕ»Θ§ΫαΚœMN=CMΦ¥Ω…Ν–≥ωΙΊ”ΎmΒΡΖΫ≥ΧΘ§ΫβΖΫ≥ΧΦ¥Ω…«σΒΟΕ‘”ΠΒΡmΒΡ÷ΒΘ§¥”ΕχΒΟΒΫΕ‘”ΠΒΡΒψQΒΡΉχ±ξ.
mΘ§»ΜΚσΖ÷ΒψN‘Ύ÷±œΏBCΒΡ…œΖΫΚΆœ¬ΖΫΝΫ÷÷«ιΩω”ΟΚ§mΒΡ¥ζ ΐ Ϋ±μ¥ο≥ωMNΒΡ≥ΛΕ»Θ§ΫαΚœMN=CMΦ¥Ω…Ν–≥ωΙΊ”ΎmΒΡΖΫ≥ΧΘ§ΫβΖΫ≥ΧΦ¥Ω…«σΒΟΕ‘”ΠΒΡmΒΡ÷ΒΘ§¥”ΕχΒΟΒΫΕ‘”ΠΒΡΒψQΒΡΉχ±ξ.
Θ®1Θ©ΓΏΕ‘≥Τ÷αx=![]() Θ§
Θ§
ΓύΒψEΉχ±ξΘ®![]() Θ§0Θ©Θ§
Θ§0Θ©Θ§
Ννy=0Θ§‘ρ”–ax2©¹3ax©¹4a=0Θ§
Γύx=©¹1Μρ4Θ§
ΓύΒψAΉχ±ξΘ®©¹1Θ§0Θ©Θ°
Ι ¥πΑΗΖ÷±πΈΣΘ®![]() Θ§0Θ©Θ§Θ®©¹1Θ§0Θ©Θ°
Θ§0Θ©Θ§Θ®©¹1Θ§0Θ©Θ°
Θ®2Θ©»γΆΦΔΌ÷–Θ§…ηΓ―E”κ÷±œΏBCœύ«–”ΎΒψDΘ§Ν§Ϋ”DEΘ§‘ρDEΓΆBCΘ§
ΓΏDE=OE=![]() Θ§EB=
Θ§EB=![]() Θ§OC=©¹4aΘ§
Θ§OC=©¹4aΘ§
ΓύDB=![]() Θ§
Θ§
ΓΏtanΓœOBC=![]() Θ§
Θ§
Γύ![]() Θ§ΫβΒΟa=
Θ§ΫβΒΟa=![]() Θ§
Θ§
Γύ≈ΉΈοœΏΫβΈω ΫΈΣy=![]() Θ°
Θ°
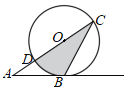
Θ®3Θ©»γΆΦΔΎ÷–Θ§”…Χβ“βΓœMΓδCN=ΓœNCBΘ§
ΓΏMNΓΈOMΓδΘ§
ΓύΓœMΓδCN=ΓœCNMΘ§
ΓύMN=CMΘ§
ΓΏΒψBΒΡΉχ±ξΈΣΘ®4Θ§0Θ©Θ§ΒψCΒΡΉχ±ξΈΣΘ®0Θ§3Θ©Θ§
Γύ ÷±œΏBCΫβΈω ΫΈΣy=©¹![]() x+3Θ§BC=5Θ§
x+3Θ§BC=5Θ§
ΓύMΘ®mΘ§©¹![]() m+3Θ©Θ§NΘ®mΘ§©¹
m+3Θ©Θ§NΘ®mΘ§©¹![]() m2+
m2+![]() m+3Θ©Θ§ΉςMFΓΆOC”ΎFΘ§
m+3Θ©Θ§ΉςMFΓΆOC”ΎFΘ§
ΓΏsinΓœBCO=![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓύCM=![]() mΘ§
mȧ
ΔΌΒ±N‘Ύ÷±œΏBC…œΖΫ ±Θ§©¹![]() x2+
x2+![]() x+3©¹Θ®©¹
x+3©¹Θ®©¹![]() x+3Θ©=
x+3ȩ=![]() mȧ
mȧ
ΫβΒΟΘΚm=![]() Μρ0Θ®…αΤζΘ©Θ§
Μρ0Θ®…αΤζΘ©Θ§
ΓύQ1Θ®![]() Θ§0Θ©Θ°
Θ§0Θ©Θ°
ΔΎΒ±N‘Ύ÷±œΏBCœ¬ΖΫ ±Θ§Θ®©¹![]() m+3Θ©©¹Θ®©¹
m+3Θ©©¹Θ®©¹![]() m2+
m2+![]() m+3Θ©=
m+3ȩ=![]() mȧ
mȧ
ΫβΒΟm=![]() Μρ0Θ®…αΤζΘ©Θ§
Μρ0Θ®…αΤζΘ©Θ§
ΓύQ2Θ®![]() Θ§0Θ©Θ§
Θ§0Θ©Θ§
Ήέ…œΥυ ωΘΚΒψQΉχ±ξΈΣΘ®![]() Θ§0Θ©ΜρΘ®
Θ§0Θ©ΜρΘ®![]() Θ§0Θ©Θ°
Θ§0Θ©Θ°