题目内容
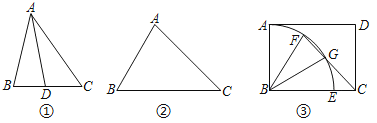
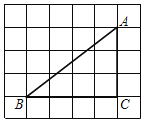
【题目】如图，在6×5的网格（小正方形边长为1）中，Rt△ABC的三个顶点都在格点上．
（1）在网格中，找到格点D，使四边形ACBD的面积为10，并画出这个四边形．
（2）借助网格、只用直尺（无刻度）在AB上找一点E，使△AEC为等腰三角形，且AE＝AC．
【答案】（1）见解析；（2）见解析
【解析】
（1）根据网格，即可找到格点D，使四边形ACBD的面积为10，并画出这个四边形；
（2）借助网格、只用直尺即可在AB上找一点E，使△AEC为等腰三角形，且AE＝AC．
（1）在点B上方两格处找到格点D，连接DA，如图，
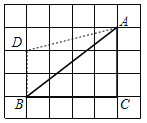
此时S四边形ADBC=S△ABD+S△ABC=
四边形ACBD即为所求；
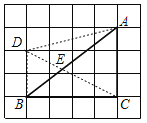
（2）连接DC与AB交于点E，点E即为所求．如图，
练习册系列答案
考前必练系列答案
相关题目
【题目】某厂按用户需求生产一种产品，成本每件20万元，规定每件售价不低于成本，且不高于40万元。经市场调查，每年的销售量y（件）与每件售价x（万元）满足一次函数关系，部分数据如下表：
售价x（万元/件） | 25 | 30 | 35 |
销售量y（件） | 50 | 40 | 30 |
（1）求y与x之间的函数表达式；
（2）设商品每年的总利润为W（万元），求W与x之间的函数表达式（利润=收入-成本）；
（3）试说明（2）中总利润W随售价x的变化而变化的情况，并指出售价为多少万元时获得最大利润，最大利润是多少？
