��Ŀ����
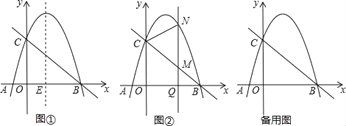
����Ŀ����ͼ��ʾ����֪���κ���y=-x2+bx+c��ͼ����x��Ľ���Ϊ��A(3��0)�͵�B����y�ύ�ڵ�C(0��3)������AC.
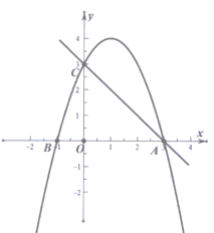
��1����������κ����Ľ���ʽ��
��2����(1)��λ�ڵ�һ�����ڵ����������Ƿ���ڵ�D��ʹ����ACD��������?�����ڣ������D�����꼰��ACD��������ֵ���������ڣ���˵������.
��3�������������Ƿ���ڵ�E��ʹ����ACE����ACΪֱ�DZߵ�ֱ��������������ڣ���ֱ��д����E�����꼴�ɣ���������ڣ���˵������.
���𰸡���1��y=-x2+2x+3����2���������ϴ��ڵ�D��ʹ����ACD��������ʱ��D������Ϊ( ![]() ��
�� ![]() )����ACD��������ֵ
)����ACD��������ֵ ![]() ����3�����������ϴ��ڵ�E��ʹ����ACE����ACΪֱ�DZߵ�ֱ��������
����3�����������ϴ��ڵ�E��ʹ����ACE����ACΪֱ�DZߵ�ֱ��������
��E��������(1��4)��(-2��-5).
��������
(1)��Ϊ��A(3��0)����C(0,3)��������y=x2+bx+c�ϣ��ɴ���ȷ��b��c��ֵ��
(2)����D��DH��x�ᣬ��D(t��-t2+2t+3)��������ͼ���ϵ��������ʾ��S��ACD=S����OCDH+S��AHD-S��AOC=![]() �������ö�����������ֵ���ɣ�
�������ö�����������ֵ���ɣ�
(3)������������ۣ��ٹ���A��AE1��AC�����������ڵ�E1����y���ڵ�F������E1C�������F�����꣬����ֱ��AE�Ľ���ʽΪy��x3��������κ����Ľ���ʽ������������⼴�ɣ��ڹ���C��CE��CA�����������ڵ�E2����x���ڵ�M������AE2�����ֱ��CM�Ľ���ʽΪy��x��3��������κ����Ľ���ʽ������������⼴��.
��1���⣺�߶��κ���y=-x2+bx+c��x��Ľ���Ϊ��A(3��0)��y�ύ�ڵ�C(0��3)
��![]()
��֮�� ![]()
��������κ����Ľ���ʽΪy=-x2+2x+3
��2���⣺��ͼ����D(t��-t2+2t+3)������D��DH��x�ᣬ����ΪH��
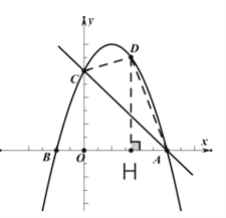
��S��ACD=S����OCDH+S��AHD-S��AOC
= ![]() (-t2+2t+3+3)+
(-t2+2t+3+3)+ ![]() (3-t)(-t2+2t+3)-
(3-t)(-t2+2t+3)- ![]() ��3��3
��3��3
= ![]()
= ![]()
�� ![]() <0
<0
�൱t= ![]() ʱ����ACD����������ֵ
ʱ����ACD����������ֵ ![]()
��ʱ-t2+2t+3= ![]()
���������ϴ��ڵ�D��ʹ����ACD��������ʱ��D������Ϊ( ![]() ��
�� ![]() )����ACD��������ֵ
)����ACD��������ֵ ![]()
��3�����������ϴ��ڵ�E��ʹ����ACE����ACΪֱ�DZߵ�ֱ��������
��E��������(1��4)��(-2��-5).
�������£������������
����ͼ��

����A��AE1��AC�����������ڵ�E1����y���ڵ�F������E1C��
��CO��AO��3��
���CAO��45����
���FAO��45����AO��OF��3��
���F��������0��3����
��ֱ��AE�Ľ���ʽΪy��kx��b��
����0��3������3��0������y��kx��b�ã�
![]()
���![]()
��ֱ��AE�Ľ���ʽΪy��x3��
��![]()
���![]() ��
��![]()
���E1��������2��5����
����ͼ��

����C��CE��CA�����������ڵ�E2����x���ڵ�M������AE2 ��
�ߡ�CAO��45����
���CMA��45����OM��OC��3��
���M��������3��0��,
��ֱ��CM�Ľ���ʽΪy��kx��b��
����0��3������-3��0������y��kx��b�ã�
![]()
���![]()
��ֱ��CM�Ľ���ʽΪy��x��3��
��![]()
��ã�![]() ��
��![]()
���E2��������1��4����
���ϣ����������ϴ��ڵ�E1��2��5����E2��1��4����ʹ��ACE1����ACE2����ACΪֱ�DZߵ�ֱ�������Σ�

 Ʒѧ˫�ž�ϵ�д�
Ʒѧ˫�ž�ϵ�д� Сѧ��ĩ���100��ϵ�д�
Сѧ��ĩ���100��ϵ�д� ��ĩ��ϰ���ϵ�д�
��ĩ��ϰ���ϵ�д� ����ѧ�䵥Ԫ������ĩר����100��ϵ�д�
����ѧ�䵥Ԫ������ĩר����100��ϵ�д�