题目内容
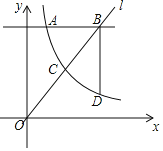
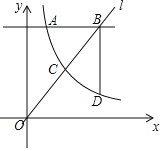
【题目】如图,反比例函数y=![]() (x>0)的图象与直线y=mx交于点C,直线l:y=4分别交两函数图象于点A(1,4)和点B,过点B作BD⊥l交反比例函数图象于点 D.
(x>0)的图象与直线y=mx交于点C,直线l:y=4分别交两函数图象于点A(1,4)和点B,过点B作BD⊥l交反比例函数图象于点 D.
(1)求反比例函数的解析式;
(2)当BD=2AB时,求点B的坐标;
(3)在(2)的条件下,直接写出不等式![]() >mx的解集.
>mx的解集.
【答案】(1)反比例函数的解析式为y=![]() .(2)B(2,4).(3)0<x<
.(2)B(2,4).(3)0<x<![]() .
.
【解析】
(1)利用待定系数法即可解决问题.
(2)设B(n,4),则D(n,![]() ),根据BD=2AB,构建方程即可解决问题.
),根据BD=2AB,构建方程即可解决问题.
(3)求出直线l与反比例函数的图象的交点C,利用图象法即可解决问题.
解:(1)∵A(1,4)在y=![]() 上,
上,
∴4=![]() ,
,
∴k=4,
∴反比例函数的解析式为y=![]() .
.
(2)设B(n,4),则D(n,![]() ),
),
∵BD=2AB,
∴4﹣![]() =2(n﹣1),
=2(n﹣1),
整理得:n2﹣3n+2=0,
解得n=1(舍弃)或2,
经检验,n=2是所列方程的解,
∴B(2,4).
(3)∵B(2,4),
∴4=2m,
∴m=2,
∴直线l的解析式为y=2x,
由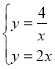 ,解得
,解得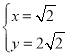 或
或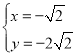 (舍弃),
(舍弃),
∴C(![]() ,2
,2![]() ),
),
观察图象可知:不等式![]() >mx的解集为0<x<
>mx的解集为0<x<![]() .
.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目