Question

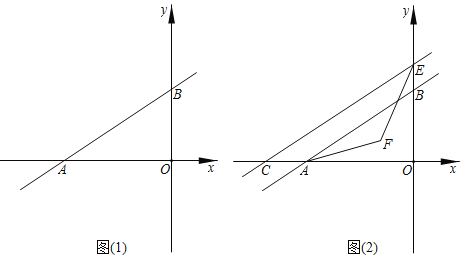
【题目】如图1，已知点是线段的中点，过点作的垂线，在射线上有一个动点(点不与端点重合)，连接，过点作的垂线，垂足为点，在射线上取点，使得，已知

(1)当时，求的度数；

(2)过点作垂直于直线交于点，在点的运动过程中，的大小随点的运动而变化，在这个变化过程中线段的长度是否发生变化？若不变，求出的长；若变化，请说明理由；

(3)如图2，当时，设直线与直线相交于点，求的度数.

Answer 1

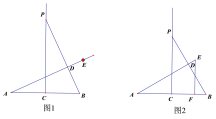
【答案】(1)15°；(2)不变，EF=4；(3)45°.

【解析】

(1)根据已知条件易得；

(2)先求出，然后可得EF=；’

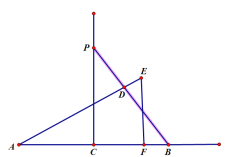
(3) 连接PA，连接PE并延长交AB的延长线于G，易得ΔAPB、ΔPAE为等腰三角形，设∠APC=∠CPB=x，∠BPG=y，所以∠APG=∠AEP=2x+y，可得，∠G=x+y；解三角形ADB可得x+y=45°即可得出∠G的度数

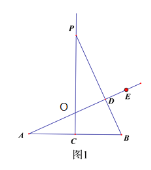
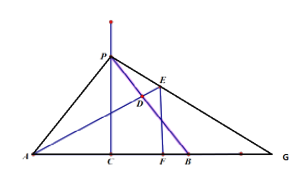
解：(1)如图，设PC与AD交点为O点.

∵PC⊥AB,AD⊥BP，

∴∠PCA=∠PDA=90°，

又∠CFA=∠PFD，

∴∠BAE=∠CPB=15°.