题目内容
【题目】正方形ABCD的边长为8,点P是边AD的中点,点E是正方形ABCD的边上一点,若![]() 是等腰三角形,则腰长为______.
是等腰三角形,则腰长为______.
【答案】5或![]() 或
或![]()
【解析】
分情况讨论:![]() 当PB为腰时,若P为顶点,则E点和C点重合,求出PB长度即可;若B为顶点,则E点为CD中点;
当PB为腰时,若P为顶点,则E点和C点重合,求出PB长度即可;若B为顶点,则E点为CD中点;![]() 当PB为底时,E在BP的垂直平分线上,与正方形的边交于两点,即为点E;
当PB为底时,E在BP的垂直平分线上,与正方形的边交于两点,即为点E;
①由题意得出![]() ,证明
,证明![]() ∽
∽![]() ,得出比例式
,得出比例式![]() ,即可求出BE;②设
,即可求出BE;②设![]() ,则
,则![]() ,根据勾股定理得出方程求出CE,再由勾股定理求出BE即可.
,根据勾股定理得出方程求出CE,再由勾股定理求出BE即可.
分情况讨论:![]() 当PB为腰时,若P为顶点,则E点与C点重合,如图1所示:
当PB为腰时,若P为顶点,则E点与C点重合,如图1所示: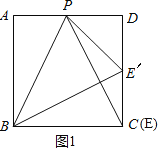
![]() 四边形ABCD是正方形,
四边形ABCD是正方形,![]() ,
,![]() ,
,![]() 是AD的中点,
是AD的中点,![]() ,
,
根据勾股定理得:![]() ;
;
若B为顶点,则根据![]() 得,
得,![]() 为CD中点,此时腰长
为CD中点,此时腰长![]() ;
;![]() 当PB为底边时,E在BP的垂直平分线上,与正方形的边交于两点,即为点E;
当PB为底边时,E在BP的垂直平分线上,与正方形的边交于两点,即为点E;
当E在AB上时,如图2所示:
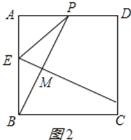
则![]() ,
,![]() ,
,![]() ,
,![]() ∽
∽![]() ,
,![]() ,即
,即![]() ,
,![]() ;
;
②当E在CD上时,如图3所示:
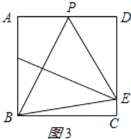
设![]() ,则
,则![]() ,
,
根据勾股定理得:![]() ,
,![]() ,
,![]() ,
,
解得:![]() ,
,![]() ,
,![]() ;
;
综上所述:腰长为:![]() ,或5,或
,或5,或![]() ;
;
故答案为:![]() ,或5,或
,或5,或![]() .
.

练习册系列答案
相关题目
【题目】(1)已知![]() ,求代数式
,求代数式![]() 的值.
的值.
(2)2018年6月武侯区某学校开展了主题为“阳光下成长,妙笔绘武侯”学生绘画书法作品比赛,要求参赛学生每人交一件作品. 现将从中挑选的40件参赛作品的成绩(单位:分)统计如下:
等级 | 成绩(用 | 频数 | 频率 |
|
|
| 0.2 |
|
| 20 |
|
|
| 12 | 0.3 |
请根据上表提供的信息,解答下列问题:
①表中![]() 的值为 ,
的值为 ,![]() 的值为 ;
的值为 ;
②将本次获得![]() 等级的参赛作品依次用标签
等级的参赛作品依次用标签![]() 表示. 学校决定从中选取两件作品进行全校展示,
表示. 学校决定从中选取两件作品进行全校展示,![]() 所代表的作品必须参展,另一件作品从
所代表的作品必须参展,另一件作品从![]() 等级余下的作品中抽取,求展示作品刚好是
等级余下的作品中抽取,求展示作品刚好是![]() 的概率.
的概率.