��Ŀ����
����Ŀ�����ı���![]() �У�
��![]() ��
��![]() ����һ�㣬
����һ�㣬![]() ��
��![]() ��
��![]() ������
������![]() ����ٶ����߶�
����ٶ����߶�![]() �˶���ͬʱ��
�˶���ͬʱ��![]() ��
��![]() ���������߶�
���������߶�![]() ������
������![]() �˶�����
�˶�����![]() �˶���
�˶���![]() �����㶼ֹͣ�˶������˶�ʱ��Ϊ
�����㶼ֹͣ�˶������˶�ʱ��Ϊ![]() ���룩��
���룩��

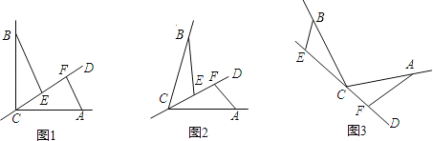
��1����![]() ��
��![]() ���ٶ���ͬ����
���ٶ���ͬ����![]() ʱ����֤��
ʱ����֤��![]()
��2����![]() ��
��![]() ���ٶȲ�ͬ����
���ٶȲ�ͬ����![]() �ֱ���
�ֱ���![]() ���˶�ʱ����ͼ1������
���˶�ʱ����ͼ1������![]() ��
��![]() ȫ�ȣ����ʱ
ȫ�ȣ����ʱ![]() ���ٶȺ�
���ٶȺ�![]() ֵ��
ֵ��
��3����![]() �˶���
�˶���![]() �ϣ�
�ϣ�![]() �˶�������
�˶�������![]() �ϣ���ͼ2������
�ϣ���ͼ2������![]() ���ٶ�Ϊ
���ٶ�Ϊ![]() �룬�Ƿ����ǡ���ı�
�룬�Ƿ����ǡ���ı�![]() �ij���ʹ���˶�������ijһʱ�̸պ�
�ij���ʹ���˶�������ijһʱ�̸պ�![]() ��
��![]() ȫ�ȣ������ڣ��������ʱ
ȫ�ȣ������ڣ��������ʱ![]() ��ֵ�ͱ�
��ֵ�ͱ�![]() �ij����������ڣ���˵�����ɣ�
�ij����������ڣ���˵�����ɣ�
���𰸡���1������������2��![]() ���ٶ�Ϊ3��t��ֵΪ2����3��
���ٶ�Ϊ3��t��ֵΪ2����3��![]() �ij�Ϊ
�ij�Ϊ![]() ʱ��
ʱ��![]() ��������ȫ��
��������ȫ��
��������
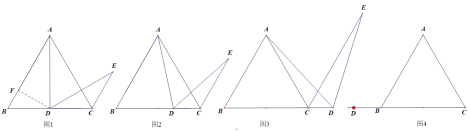
��1������SAS����֤����EBP�ա�PCQ��
��2����ȷѰ��ȫ�������εĶ�Ӧ�ߣ�����·�̣��ٶȣ�ʱ��Ĺ�ϵ���ɽ�����⣮
��3�����������ηֱ������鼴�ɽ�����⣮
��1�������⣺BP=CQ=1��2=2��cm����
��BC=8cm��BE=6cm��
��PC=8-2=6��cm����
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]()
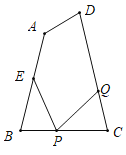
��2����![]() ���ٶ�Ϊ
���ٶ�Ϊ![]() ��
��
��![]() ��
��
�����������
�ٵ�![]() ʱ��
ʱ��![]() ��
��
��![]() ����ã�
����ã�![]() ����ȥ��
����ȥ��
�� ��![]() ʱ��
ʱ��![]() ��
��
��![]() ����ã�
����ã�![]()
Q���ٶ�Ϊ3��t��ֵΪ2.
��3����![]() ����
����![]() ��
��

�����������
�ٵ�![]() ʱ��
ʱ��![]() ��
��
��![]() ����ã�
����ã�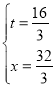
��![]() ��
��![]()
��![]() �����
�����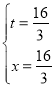
�ʣ���![]() �ij�Ϊ
�ij�Ϊ![]() ʱ��
ʱ��![]() ��������ȫ�ȣ�
��������ȫ�ȣ�