题目内容
【题目】如图,为了测量山坡上一棵树PQ的高度,小明在点A处利用测角仪测得树顶P的仰角为450 ,然后他沿着正对树PQ的方向前进10m到达B点处,此时测得树顶P和树底Q的仰角分别是600和300,设PQ垂直于AB,且垂足为C.
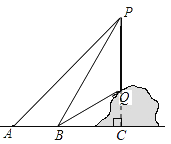
(1)求∠BPQ的度数;
(2)求树PQ的高度(结果精确到0.1m, ![]() )
)
【答案】(1)∠BPQ=30°;(2)树PQ的高度约为15.8m.
【解析】 (1)根据题意题可得:∠A=45°,∠PBC=60°,∠QBC=30°,AB=100m,在Rt△PBC中,根据三角形内角和定理即可得∠BPQ度数;
(2)设CQ=x,在Rt△QBC中,根据30度所对的直角边等于斜边的一半得BQ=2x,由勾股定理得BC=![]() x;根据角的计算得∠PBQ=∠BPQ=30°,由等角对等边得PQ=BQ=2x,用含x的代数式表示PC=PQ+QC=3x,AC=AB+BC=10+
x;根据角的计算得∠PBQ=∠BPQ=30°,由等角对等边得PQ=BQ=2x,用含x的代数式表示PC=PQ+QC=3x,AC=AB+BC=10+![]() x,又∠A=45°,得出AC=PC,建立方程解之求出x,再将x值代入PQ代数式求之即可.
x,又∠A=45°,得出AC=PC,建立方程解之求出x,再将x值代入PQ代数式求之即可.
(1)依题可得:∠A=45°,∠PBC=60°,∠QBC=30°,AB=10m,
在Rt△PBC中,
∵∠PBC=60°,∠PCB=90°,
∴∠BPQ=30°;
(2)设CQ=x,
在Rt△QBC中,
∵∠QBC=30°,∠QCB=90°,
∴BQ=2x,BC=![]() x,
x,
又∵∠PBC=60°,∠QBC=30°,
∴∠PBQ=30°,
由(1)知∠BPQ=30°,
∴PQ=BQ=2x,
∴PC=PQ+QC=3x,AC=AB+BC=10+![]() x,
x,
又∵∠A=45°,
∴AC=PC,
即3x=10+![]() x,
x,
解得:x=![]() ,
,
∴PQ=2x=![]() ≈15.8(m),
≈15.8(m),
答:树PQ的高度约为15.8m.

练习册系列答案
相关题目